-"а - Ъу

(сИ,+А) =0. (98)

В пространственной задаче в левой части уравнения добавляется еще один член

д dz

(cH, + A)f

Решение уравнения (98) теоретически вполне возможно, если задано распределение температуры д{у, z) в начальном поперечном сечении ж = О, а также температура на стенке для всех значений ж > О или совпадающая с ней температура слоя жидкости, прилегающего к стенке. Однако практически решение уравнения (98) весьма затруднительно. Проще всего оно выполнимо для ламинарного течения, при котором Aq = 0. Для случая течения в трубе с параболоидальным распределением скоростей, одинаковым для всех ж, и с постоянной температурой на стенке такое решение было впервые дано Гретцом и затем вновь, независимо от Гретна, Нуссельтом. Пусть стенки трубы имеют температуру •д, а жидкость притекает к начальному поперечному сечению ж = О с температурой •di. В связи с тем, что для образования параболического профиля скорости требуется разгон течения на начальном участке (см. стр. 227), примем, что поперечному сечению ж = О предшествует отрезок трубы подходящей длины со стенками, не проводящими тепла; следовательно, на протяжении этого отрезка развивается параболический профиль скоростей, но температура жидкости •dl остается неизменной.

Начиная от сечения ж = О вследствие соприкосновения с хорошо проводящей тепло стенкой образуется тепловой пограничный слой, при посредстве которого изменение температуры постепенно передается вплоть до середины трубы. Затем, после некоторого переходного участка, разность между температурами стенки и потока начина-

GratzL., Ann. d. Physik u. Chem., новая серия, т. 18 (1883), стр. 79, и т. 25 (1885), стр. 337.

Nusselt W., VDI-Zeitsche., т. 54 (1910), стр. 1155

06 этом в годы написания работ Гретца и Нуссольта еще не было известно.

Для дальнейшего упрощения примем, что поток в трубе движется строго параллельно стенке и что скорость и зависит только от у. Тогда для плоской задачи из уравнения (97), на основании сказанного выше, получим следующее дифференциальное уравнение распределения температуры:

г? = г?о + 1,477(г?1 - г?о)е """ . (99)

Величина

Л «

входящая в показатель степени при е, безразмерна и обладает такой же структурой, как и число Рейнольдса. В самом деле, величина

называемая температуропроводностью, имеет такую же размерность LT~, как и кинематическая вязкость v. Число Ре было введено в расчеты Гребером и названо им числом Пекле, по имени французского ученого, впервые использовавшего работы Фурье о теплопроводности для технических приложений. На рис. 307 изображена диаграмма распределения температуры при ламинарном течении в трубе. Для построения этой диаграммы использованы новые точные вычисления Ямагаты).

С технической точки зрения весьма важен вопрос о вычислении количества тепла, передаваемого в единицу времени от стенок трубы в жидкость или наоборот. Для этого вычисления можно воспользоваться условием неразрывности потока тепла и уравнением (89). Тогда количество тепла Q, переданное на участке от ж = ж1 до ж = жг от стенок в жидкость или наоборот, получится как разность между полным потоком тепла через сечение х = Xi и полным потоком тепла через сечение ж = ж2. Если не учитывать, что СрИ р зависят от температуры (так было сделано и выше, при вычислении распределения температуры), то мы получим:

Q = Qi-Q2 = CpP Л и(г?1 - e2)dF. (100)

ijamagataK., Mem. Fac. Engg. Kyushu Imp. Univ., т. 8 (1936/40), стр. 365.

ет уменьшаться по показательному закону в соответствии с уравнением (96) или графиком, на рис. 306. Гретц и Нуссельт получили свои решения в виде рядов, каждый член которых, за исключением первого, представляет собой произведение некоторой функции от на показательную функцию от X. Для середины трубы, если сохранить из всех членов ряда только первые два, решение принимает вид:

-14,63-

С другой стороны, количество тепла Q можно вычислить непосредственно как передачу тепла через стенки посредством теплопроводности, т.е. на основании уравнения

\ on J стенка

В ЭТОМ случае мы получим:

JJ van/стенка

(101)

(102)

где dF есть элемент площади стенки. Это соотношение применимо для вычисления Q также и при турбулентном течении, так как непосредственно около стенки коэффициент Ад = 0.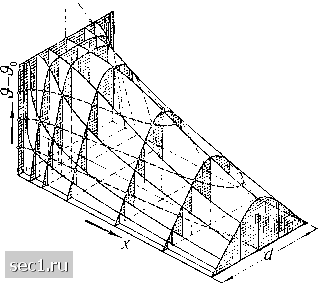

Рис. 307. Распределение температуры в трубе. Профили температур, вычерченные сплошными линиями, соответствуют значениям =0,005; 0,01;

0,02; 0,04; 0,06; 0,08. Линия, вычерченная штрих-пунктиром, является графиком уравнения (99)