Ниже, в §9, мы увидим, что равенство (21) выражает собой условие, при котором так называемая циркуляция вдоль прямоугольника, образованного дугами двух соседних линий тока и отрезками ds двух радиусов кривизны, равна нулю. Там же мы увидим, что при циркуляции, равной нулю, отдельные частицы жидкости движутся без вращения. Следовательно, равенство (21) показывает, что при нашем криволинейном течении частицы жидкости не совершают вращения.

Для примера рассмотрим движение в спиральной камере, изображенной на рис. 36. Все линии тока начинаются в параллельном потоке в области А, в которой скорость и давление везде одинаковы, следовательно, постоянная в уравнении Бернулли, составленного для потока в спиральной камере, одинакова на всех линиях тока. Радиусы кривизны отдельных линий тока можно считать приближенно равными радиусу г, проведенному из центра камеры О, поэтому можно принять, что ds = dr. Тогда уравнение (21) примет вид: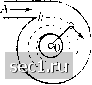

Рис. 36. Течение в спиральной камере

dw I w г dr г -

откуда после интегрирования мы получим:

In w = In С - In г.

где С есть постоянная интегрирования. Следовательно, скорость течения по мере приближения к центру камеры сильно возрастает. Подставив найденное выражение скорости w в уравнение Бернулли (19), мы найдем давление:

р = const--.

При постоянной высоте камеры радиальная составляющая скорости вследствие неразрывности потока также обратно пропорциональна радиусу г, поэтому угол, образуемый линиями тока с радиусами, везде одинаковый, следовательно, линиями тока являются логарифмические спирали.

Если поток внутри камеры, достигнув радиуса п, выходит через сделанное здесь отверстие в свободную атмосферу, где давление равно ро, то здесь предыдущее уравнение дает нам:

Ро = const -

рС 2г1

Исключив из обоих уравнений постоянную (const), мы получим

Р=Ро+ Р

Следовательно, если выходное отверстие внутри камеры мало, то при входе в камеру давление может сделаться очень большим.

с) При неустановившихся движениях для получения связи между давлением и скоростью вдоль линии тока следует проинтегрировать

уравнение (8), не отбрасывая члена Бернулли (9) мы получим:

. Поэтому вместо уравнения

j>+gz +

dw dt

ds = const.

(22)

£

ft-

Ч EzPo

/

В случае движения в трубе с постоянным поперечным сечением скорость течения в каждый определенный момент времени одинакова во всех сечениях; кроме того, она одинакова также во всех точках каждого сечения, поскольку мы предполагаем, что жидкость не обладает трением. В таком случае произ-dp

водная не зависит от s, и интеграл в левой части уравнения (22) будет равен s.

Для примера рассмотрим начальную стадию истечения из сосуда через насадок длиной / (рис. 37). Применяя уравнение (22) к горизонтальной линии тока, совпадающей с осью насадка, мы получим для точки В, находящейся на расстоянии s от входа в насадок, уравнение

Рис. 37. Истечение из насадка

откуда

dt ~ I V*" 2 В первый момент истечения w = О, следовательно.

dw 1 („I, w \

По мере увеличения w производная все более и более уменьшается,

пока не делается равной нулю. В этот момент течение превращается в установившееся, и скорость истечения принимает значение

Нетрудно вывести точный закон изменения скорости w в зависимости от времени, однако мы этим заниматься не будем. Для оценки времени, которое требуется для того, чтобы течение сделалось приблизительно установившимся, следует принять что ускорение остается

а для точки А около входа в насадок (s = 0) - уравнение

Приравнивая левые части уравнений и имея в виду, что величиной v)\ можно пренебречь как весьма малой по сравнению с и что

РА=Ро+ gph,

где Ро есть давление на свободной поверхности, мы получим:

-р + + =-р+-

До тех пор, пока не равно нулю, давление уменьшается вдоль на-dt

садка пропорционально расстоянию s. Для концевого сечения насадка (s = I), в котором давление равно ро, уравнение (22) дает:

Ро w , dw, Ро , ,