а из уравнения (28) - соотношение

причем отрезок dh, согласно сказанному выше, перпендикулярен к поверхности Ф = const. Из равенства (29) следует, что наибольшее изменение потенциала Ф происходит в направлении нормали к поверхности Ф = const. Это наибольшее изменение, равное называется градиентом потенциала Ф и обозначается через gradФ. Градиент представляет собой векторную величину. Так как вектор скорости w, согласно сказанному выше, перпендикулярен к поверхности Ф = const, то из равенства (30) следует, что скорость течения по величине и направлению равна градиенту потенциала Ф. В векторной форме равенство (30) записывается следующим образом:

W = gradФ. (31)

Введенное нами геометрическим путем понятие потенциала совпадает с понятием потенциала сил, с той только разницей, что градиент потенциала сил равен напряженности силового поля, а градиент нашего потенциала равен скорости течения. Поэтому введенный нами потенциал называют, в отличие от потенциала сил, потенциалом скоростей, или потенциалом течения. Заметим, что между обоими потенциалами имеется еще одна, чисто условная разница: обычно принимают, что напряженность силового поля равна

g = -gradf/,

а скорость течения равна

W = -\- gradФ.

Можно было бы перед gradФ взять знак минус и тем самым обеспечить более полную аналогию с потенциалом сил. Так иногда и делается, однако для гидродинамических расчетов удобнее брать перед gradФ знак плюс, что мы в дальнейшем и будем делать.

Из всего сказанного следует, что при всяком движении однородной жидкости без трения, возникающем из состояния покоя, существует функция, называемая потенциалом и обладающая тем свойством, что ее градиент определяет скорость течения в любой точке потока. Движения жидкости, обладающие потенциалом скоростей, называются потенциальными течениями. При потенциальных течениях частицы жидкости не совершают вращения, что и является отличительным

Если, кроме вращательного движения, жидкость обладает также поступательным движением, то последнее не надо учитывать, так как оно не влияет на циркуляцию. Разделив циркуляцию на площадь окружности F = 7гг, мы получим:

l=2w.

Следовательно, величиной - удобно пользоваться в качестве меры вращения жидкости.

Если площадка расположена в плоскости, образующей с осью вращения угол а, то, как нетрудно видеть,

= 2wsina. (32)

Таким образом, максимальное значение получается в плоскости, пер-

пендикулярной к оси вращения.

Итак, при потенциальном течении циркуляция вдоль любой замкнутой линии, проведенной внутри жидкости, равна нулю, следовательно, частицы жидкости движутся без вращения. В прежнее время отсюда пытались вывести как следствие, что при движениях однородной, лишенной трения жидкости, возникших из состояния покоя, никогда не могут возникнуть вихри. Однако, если мы более внимательно рассмотрим процесс движения при образовании поверхности раздела (§7), то окажется, что все жидкие линии, проведенные внутри жидкости в состоянии покоя, движутся и деформируются так, что ни одна из них не

свойством таких течений. В самом деле, мерой вращения частицы может служить циркуляция вдоль небольшой замкнутой кривой, но эта циркуляция в течениях однородных жидкостей без трения, возникающих из состояния покоя, согласно сказанному выше, равна нулю.

В качестве противоположного примера рассмотрим жидкость, которая вращается как твердое тело с угловой скоростью вокруг некоторой оси. Возьмем в плоскости, перпендикулярной к оси вращения, площадку в виде окружности радиуса г с центром на оси вращения и вычислим циркуляцию вдоль этой окружности. Так как линейная скорость течения в точках окружности равна wr и направлена по касательной к окружности, то

Г = ф W • ds = ф wr • г dip = wrftpln = 27гг№.

пересекает поверхности раздела. Поэтому теорема Томсона не позволяет сделать никаких заключений о взаимоотношении между частями жидкости, лежащими по разные стороны от поверхности раздела. Следовательно, возникновение в жидкости, практически лишенной трения, поверхностей раздела, а вместе с ними и вихрей, нисколько не противоречит теореме Томсона.

В реальных жидкостях, которые всегда обладают вязкостью, вместо поверхностей раздела образуются слои раздела, правда, обычно очень тонкие. Слой раздела всегда образуется из частиц, двигающихся в непосредственной близости от поверхности твердого тела, где влиянием трения нельзя пренебрегать даже при очень малой вязкости. Поэтому точный анализ явлений, происходящих внутри слоя раздела, возможен только на основе учета вязкости. Для изучения явлений, происходящих вне слоя раздела, но связанных с его существованием, обычно достаточно рассматривать вместо слоя раздела поверхность раздела. Влияние трения будет подробно рассмотрено в § 1-6 гл. III.

Рассматривая в § 6 течение, в котором постоянная Бернулли для всех линий тока одинакова, мы нашли, что в направлении, перпендикулярном к линии тока, скорость изменяется согласно уравнению

dw ds

w - О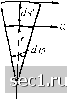

dw , , w+ -j-r as ds

Рис. 54. Четырехугольник, вдоль которого вычисляется циркуляция

где г есть радиус кривизны линии тока. Вычислим циркуляцию вдоль небольшого четырехугольника, образованного дугами двух соседних линий тока и отрезками двух смежных нормалей (рис. 54). Мы получим:

Т = wrdLp + (i-ds - (+ Ipcs {г + ds)dLp -Q-ds =

= -ds .d{T,+w+ ,ds\ .

V ds ds J

Последний член в скобках можно отбросить как величину более высокого порядка малости по сравнению с первым членом, сумма же первых двух членов равна нулю согласно приведенному выше равенству. Таким образом, при рассмотренном движении циркуляция вдоль любой замкнутой малой кривой равна нулю, следовательно, это движение потенциальное. Обратно, можно доказать (см. ниже), что если течение