Все выражения в квадратных скобках можно проинтегрировать, не налагая никаких ограничений на путь интегрирования. В результате мы получим:

§ + "+"+"4p+U = const. (39)

Так как интегрирование выполнено нами для определенного момента времени, то постоянная в правой части уравнения (39) в разные моменты времени может принимать, вообще говоря, разные значения (например, в том случае, когда давление в пространстве, занимаемом жидкостью, изменяется путем внещнего воздействия). Поэтому правильнее в правой части написать /(i)

вместо const. Если движение установившееся, то = О, и уравнение (39)

переходит в уравнение Бернулли.

§10. Потенциальное течение (продолжение). Полагая в уравнении (29) ds последовательно равным dx, dy и dz, мы найдем соотношения, связывающие составляющие скорости и, v, w с потенциалом скоростей Ф:

-f- «

Подставляя эти выражения и, v, w в уравнение неразрывности

ди &V &W Q дх ду dz

мы получим так называемое уравнение Лапласа:

дЧ ,дЧ ,дЧ f.-..

Это уравнение встречается также в других областях физики, в частности, в электростатике - в учении об электростатическом потенциале, где оно выполняется в таких местах поля, в которых отсутствуют заряды и диэлектрическая постоянная имеет постоянное значение. Поэтому при решении гидродинамических задач могут быть непосредственно использованы решения уравнения (41), известные из электростатики, например, решения для точечного заряда, для диполя и т. д. Для практических приложений важное значение имеет следующее свойство уравнения Лапласа: сумма или разность двух его решений также является решением, что непосредственно следует из линейности этого уравнения. При таком «наложении» двух потенциалов скорости складываются по закону параллелограма. Заметим, что уравнение Лапласа выполняется также для течения вязкой жидкости между двумя параллельными

Тогда мы получим:

b = а, с = -2а.

Ф=1(х + у-2г), (44)

откуда найдем составляющие скорости течения:

и = ах, V = ау, w = -2az.

Очевидно, что поток, определяемый этим потенциалом, симметричен относительно оси вращения, совпадающей в осью z. Линии тока в плоскости yz, где ж = О, определяются диференциальным уравнением

dz W 2z dy~ V ~ У

интегрируя которое, мы получим:

\nz = const - 2 In у,

yz = const.

Это уравнение изображает так называемую кубическую параболу (рис. 55), для которой оси z и у являются асимптотами. Таким образом, потенциал скоростей (44) определяет трехмерный, симметричный относительно оси, поток перед пластинкой.

пластинками, поставленными близко друг от друга. Такое течение часто используется для демонстрации линий тока потенциального течения (см. §9 гл. III). Хотя в действительности оба течения формируются разными силами, тем не менее линии тока того и другого течения при надлежащих условиях опыта весьма точно совпадают.

Рассмотрим несколько примеров потенциального течения.

а) Трехмерный поток перед пластинкой. Одним из самых простых выражений для потенциала скоростей будет следующее:

Ф={ах + Ьу + cz). (42)

Подставляя это выражение Ф в уравнение Лапласа (41), мы получим:

а + Ь+с = 0. (43)

Следовательно, для того чтобы функция (42) удовлетворяла уравнению Лапласа, коэффициенты а, b и с должны удовлетворять условию (43). Это условие можно выполнить, приняв

Если движение установившееся, т.е. если коэффициент а не зависит от времени, то давление в потоке равно

р = const - {и + + w) =

= const - (ж + + 42;).

Следовательно, максимум давления получается в точке ж = у = 2; = О, т. е. в начале координат. Поверхности равного давления представляют собой эллипсоиды с осями, длины которых относятся как 1 : 2 : Уз (рис. 55).

Ъ) Источник и сток. Функция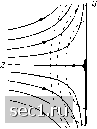

Рис. 55. Трехмерный симметричный относительно оси поток перед пластинкой

(45)

где г = + у2 2 означает расстояние от начала координат, удовлетворяет уравнению Лапласа (41), а потому определяет потенциальное течение. Так как поверхности Ф = const представляют собой концентрические сферы и так как скорость течения w перпендикулярна к поверхностям Ф = const, то в потоке, определяемом потенциалом скоростей (45), скорость во всех точках направлена вдоль радиуса и равна

= = дг

Поток, определяемый потенциалом скоростей Ф = называется источником, а поток, определяемый потенциалом Ф = - - стоком. Линиями тока источника являются прямые, исходящие из начала координат, а линиями тока стока - прямые, сходящиеся в начале координат. И в источнике и в стоке скорость в начале координат равна бесконечности.

Количество жидкости, протекающее в источнике или стоке в единицу времени через сферу радиуса г, поверхность которой имеет площадь 47гг, равно

Q = 47гг • = 47гс.

(46)

В источнике это количество возникает в центре, а в стоке, наоборот, исчезает в центре. Величина Q называется мощностью источника или