стока. Конечно, осуществить такое течение физически нельзя. Однако если в какую-нибудь точку О объема, занятого жидкостью, подвести узкую трубочку и отсасывать через нее жидкость, то в окрестности точки О возникнет поток, приближенно совпадающий со стоком.

Источники и стоки играют важную вспомогательную роль при гидродинамических расчетах. Например, если в жидкости движется удлиненное тело в направлении своей продольной оси (рис. 56), то его передний конец вытесняет перед собой жидкость, к заднему же концу, по мере его продвижения вперед, жид-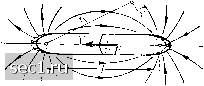

Рис. 56. Потенциальный поток около движущегося тела

кость притекает. Следовательно, около концов тела движение жидкости такое, как если бы около переднего конца был источник, а около заднего конца - сток. В самом деле, потенциал скоростей

получаемый наложением источника и стока, дает именно такую картину течения жидкости, правда при условии, что концы тела имеют определенную, хорошо округленную форму. Однако указанный потенциал дает достаточно хорошее приближение и при другой форме концов тела. Если тело движется со скоростью V, а площадь его поперечного сечения равна F, то количество вытесняемой телом и вновь притекающей к телу жидкости можно положить равным Q = FV. Подставляя это значение Q в формулу (46), мы найдем постоянную с:

FV 47Г

Рассматриваемый поток жидкости, очевидно, неустановившийся, так как вместе с перемещением тела перемещается и поле скоростей в жидкости. Но если это течение рассматривать в системе отсчета, относительно которой тело покоится, т.е. в системе отсчета, движущейся вместе с телом, то в такой системе отсчета жидкость обтекает тело, и поток будет установившимся. Математически такой установившийся поток определяется потенциалом скоростей

Ф = Ф + Vx.

Рис. 57. Поток около движущегося тела. Рис. 58. Потенциальный по-Система отсчета движется вместе с телом ток около шара

Его линии тока изображены на рис. 57. Кривая внизу рисунка показывает распределение давления на поверхности, найденное на основании уравнения Бернулли.

Будем сближать между собой источник и сток, причем одновременно будем увеличивать их мощность в таком же отношении, в каком уменьшается их расстояние друг от друга. В пределе мы получим поток, называемый диполем. При таком сближении источника и стока поток, изображенный на рис. 57, переходит в поток около шара (рис. 58). Потенциал скоростей для такого потока равен

Ф = Vx(l+-

где а есть радиус шара. Картина действительного обтекания шара имеет вследствие влияния трения несколько иной вид.

с) Плоское движение. Если при движении жидкости все линии тока представляют собой плоские кривые, расположенные в параллельных плоскостях, и скорость течения во всех точках каждой прямой, перпендикулярной к семейству параллельных плоскостей, одинаковая, то такое движение жидкости называется плоскопараллельным, или плоским движением. Если совместить одну из параллельных плоскостей с плоскостью ху, то из трех составляющих скорости и, v, w последняя будет равна нулю, а первые две будут функциями только от ж и у. В математической гидродинамике теория плоских потоков разработана особенно полно, так как существует мощный математический метод, облегчающий исследование таких потоков. Оказывается, что и вещественная, и мнимая части любой аналитической функции комплексной переменной X + iy всегда удовлетворяют уравнению Лапласа (41) и поэтому могут рассматриваться как потенциалы. В самом деле, пусть функция

F{z) = Ф -Ь гФ

поэтому

то должны соблюдаться условия:

= (=«), l = -{=v). (47)

dx dy dy dx

тие Лапласа (41), которое 2 =0 состоит теперь только из двух членов, мы получим:

Составляя уравнение Лапласа (41), которое вследствие равенства

дФ , dФ аФ аФ

dy dydx dxdy

= 0,

dd4 d dQ dx" dy dydx dxdy

т.е. обе функции Ф и Ф действительно удовлетворяют уравнению Лапласа и, следовательно, могут рассматриваться как потенциалы скоростей некоторых двух потоков.

Нз соотношений (47) легко видеть, что оба эти потока в каждой точке ортогональны друг к другу и имеют здесь равные по абсолютной

есть аналитическая функция комплексного переменного z = х + iy, причем Ф есть вещественная часть функции, а Ф - мнимая часть. Мы имеем:

OFdFdz dFdF d дх dz дх ду dz ду

= 1 = г дх ду

dFdF IdF dz dx i dy

Подставляя сюда F = Ф + гФ, мы получим:

dx dx г dy dy

Для того чтобы это равенство соблюдалось, должны совпадать между собой отдельно его вещественные части и отдельно мнимые части. Следовательно, если учесть, что