следовательно.

tg/3 = -

Абсолютная величина скорости и в первом и во втором потоке равна л/и + v. Вследствие ортогональности обоих потоков линии равного потенциала одного потока являются линиями тока другого (скорость всегда направлена по нормали к поверхности равного потенциала).

Функция, значения которой остаются постоянными на линиях тока, называется функцией тока. Следовательно, если функция Ф выбрана в качестве потенциала скоростей, то Ф будет функцией тока. Функция тока имеет еще другое наглядное зачение: разность ее значений в двух точках равна объему жидкости, протекающему в единицу времени между обеими точками в слое с толщиной, равной единице.

Рассмотрим несколько примеров плоских потоков. Плоский поток перед стенкой определяется функцией

В самом деле, мы имеем:

ф + гФ= (ж-ь2га;у-Г),

следовательно,

Ф=(ж-2/), Я> = аху.

величине скорости. В самом деле, скорость первого потока образует с осью X угол а, для которого

ду у дх

скорость второго потока образует с осью х угол /3, для которого

tg/3 =

Последнее уравнение показывает, что линиями тока Ф = const являются равнобочные гиперболы, асимптотами которых служат оси х и у. Составляющие скорости равны

дФ дФ

Плоский источник определяется функцией

F = blnz.

Так как

Z = X + iy = г (cos ip + sin ip) = re", где г и if суть полярные координаты, то

\nz = Inr + iifi,

следовательно,

Ф = & lnr, = bip.

Таким образом, линиями тока Ф = const действительно являются прямые if, исходящие из начала координат. Линиями равного потенциала Ф = const являются окружности г = const.

в качестве третьего примера рассмотрим поток вдоль двух пересекающихся между собой стенок. Такой поток, если точка пересечения стенок расположена в начале координат, а ось х направлена вдоль одной из стенок, определяется функцией

F = - z"

где п = ; а есть угол между обеими стенками. В самом деле, введя полярные координаты, мы получим:

fz" = r"[r(cos + «sin)]", или, на основании формулы Муавра,

jz" = jr"(cos п(р + г sin п(р). Следовательно, функцией тока будет

Ф = г" sini.

Она принимает нулевое значение Ф = О, т.е. совпадает со стенкой, при следующих значениях ip:

или, если заменить п указанным выше его значением, при

(fi = О, а, 2а, ...

Таким образом, при разных значениях п = мы будем иметь потоки вдоль двух стенок, пересекающихся между собой под углами а. На рис. 59 изображены линии тока таких потоков, получающихся для значений а = , , 7г, 7г и 2ж. Как легко видеть, для углов а < ж скорость течения в начале координат равна нулю, а для углов а > ж она равна бесконечности.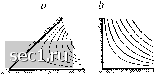

a=f ,F=A-z* а= ,F=A-z

a=n;F=A-z

a= 3 я,Р=А а=2я,Р=А

Рис. 59. Потоки, определяемые функцией F = Az" при разных значениях п

Поток около круглого цилиндра радиуса а в направлении, перпендикулярном к оси цилиндра, определяется функцией

F = V

Вычисляя функцию тока Ф, мы получим:

= Vsm(r- . Она равна нулю на оси х, где sini = О, и на окружности радиуса г,

где г - = 0. Картина линий тока получается очень похожей на картину линий тока при обтекании шара (см. рис. 58).

Можно было бы привести еще много других примеров плоских потоков, определяемых функциями комплексной переменной, но мы ограничимся разобранными. В теории функций комплексной переменной