существует метод, позволяющий из известного потока около какого-нибудь тела получать новые потоки около других тел. Будем рассматривать две комплексные переменные z = х + гу и ( = + гг]. Каждой паре значений х, у соответствует точка в плоскости ху, а каждой паре значений , г] - точка в плоскости г]. Всякая функция

Z = /(С)

устанавливает между z и ( соответствие такого рода, что каждая пара значений , rj связывается с парой значений х, у, следовательно, каждая точка плоскости г] связывается с точкой плоскости ху. Такое соответствие между плоскостями rj и ху называют отображением. При отображении каждая линия плоскости ху переходит в некоторую линию плоскости rj, точка пересечения двух линий плоскости ху - в точку пересечения соответствующих линий в плоскости т]. Производные от вещественной и мнимой частей функции удовлетворяют соотношениям такого же вида, как и равенства (47). Прямоугольная сетка одной плоскости отображается также в прямоугольную, но в общем случае криволинейную сетку другой плоскости, причем масштаб отображения в обоих направлениях получается одинаковым. Это означает, что в бесконечно малых частях отображение происходит с соблюдением подобия. Поэтому такого рода отображения называются конформными отображениями. Примеры плоских потоков, разобранные выше, одновременно являются и примерами конформных отображений, если только вместо Ф и Ф написать и т]. Последний из примеров показывает, что функция

F = v[z+l

отображает полуплоскость ФФ на область плоскости ху, ограниченную двумя отрезками оси х, простирающимися от -оо до -а и от +а до Ч-оо, и половиной окружности радиуса а.

Важное значение конформных отображений для гидродинамики состоит в следующем. Если F есть аналитическая функция от z, а z есть аналитическая функция от (, то F есть аналитическая функция также и от (. Это означает, что в плоскости ( функция F = Ф-ЬгФ также определяет некоторый поток. Следовательно, если в плоскости ху имеется какой-нибудь поток, что всякое конформное отображение плоскости ху на плоскость г] дает некоторый новый поток. Такой способ получения новых потоков из заданного потока может быть повторен сколько угодно раз.

Существуют различные методы, позволяющие конформно отобразить область плоскости г], лежащую вне контура, близкого по форме к профилям современных крыльев самолета, на область плоскости ху, лежащую вне окружности. Картина линий тока и динамические соотношения при обтекании окружности известны, поэтому, зная вид отображающей функции, можно из этой картины легко получить все, что относится к обтеканию профиля крыла.

Производная

как легко видеть, равна

dF dz

= и - IV.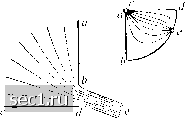

Эта величина, сопряженная с величиной и + iv, называется комплексной скоростью и обозначается через w. Очевидно, что w является аналитической функцией от Z или от F, следовательно, отображение плоскости ФФ на плоскость uv также является кон-

. Рис. 60. Истечение через щель

формным. Существуют такие случаи,

когда, не зная функции F{z), определяющей поток в плоскости ху, можно тем не менее заранее, на основании заданных граничных и других условий, построить картину распределения комплексной скорости w в плоскости UV. Так, например, при истечении жидкости через щель между двумя стенками (рис. 60а) заранее известны направления скорости на стенках аЬ и cd; далее известно, что на границах свободной струи скорость постоянна (это следует из уравнения Бернулли, так как на границах струи давление одинаковое); наконец, нам известны предположительные направления линий тока до истечения из щели, а также предположительное направление струи после истечения. На основании этих данных мы можем построить в плоскости uv картину распределения скоростей (рис. 60,6) и рассматривать ее как некоторый поток. Если для этого потока функция

F = Fiw),

его определяющая, известна, то можно путем обращения найти функ-

Подробности и указания на литературу можно найти в книгах: Schmidt Н., Aerodynamik des Fluges, Berlin, 1929; Miiller W., Mathematische Stromungslehre, Berlin, 1928. [См. также Лаврентьев M.A., Конформные отображения с приложениями к некоторым вопросам механики. Москва, 1947. (Прим. перев.)]

мы получим:

z=

w{F)

Наконец, отделив вещественную и мнимую части комплексной переменной Z, мы найдем для каждого значения Ф и Ф соответствующие им значения х, у, т.е. построим картину линий тока.

Приведенных примеров достаточно, чтобы дать представление о применении методов теории функции комплексной переменной в гидродинамике.

§ 11. Потенциальное течение с циркуляцией. Подъемная сила крыла. Эффект Магнуса. Хотя при всех потенциальных течениях циркуляция в любой малой области потока равна нулю, тем не менее существуют такие потенциальные потоки, в которых циркуляция для всего потока в целом не равна нулю. Правда, необходимым условием для этого является многосвязность области, в которой происходит течение. Область пространства или плоскости называется многосвязной, если в ней можно провести такие замкнутые кривые, которые нельзя стянуть в точку, не разрывая их, т.е. не выходя за пределы области. Примерами двухсвязной области могут служить комната с колонной посредине или область вокруг кольца. Пусть поток занимает многосвязную область, в каждой односвязной части которой частицы движутся без вращения, следовательно, в каждой такой части циркуляция равна нулю. Далее, пусть в рассматриваемой области циркуляция вдоль какой-нибудь кривой, которую нельзя стянуть в точку, равна Г. Тогда, как легко доказать, циркуляция вдоль любой другой кривой, которую нельзя стянуть в точку и которая получается из первой непрерывной деформацией, также равна Г. В § 10 мы определили потенциал в заданной точке как значение криволинейного интеграла при интегрировании между фиксированной точкой и заданной точкой. Поскольку теперь в потоке существуют замкнутые кривые, вдоль которых циркуляция не равна нулю, а имеет некоторое значение Г, то это означает, что потенциал такого потока не является больше однозначным; наоборот.

W = w{F). Тогда, проинтегрировав уравнение