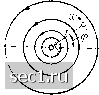Рис. 61. Потенциальный поток с циркуляцией

Рис. 62. Полый вихрь

теперь он является многозначным, увеличиваясь при каждом обходе нестягиваемой в точку кривой на величину Г.

Простейший плоский поток такого рода определяется потенциалом скоростей

Ф = cip,

где (р есть центральный угол (рис. 61). Этот потенциал, удовлетворяющий, как легко видеть, уравнению (41), возрастает при каждом полном обходе замкнутой нестягиваемой в точку кривой {(р2 = + Зтг) на величину 27гс, которая, следовательно, и является циркуляцией Г. Поверхностями равного потенциала являются плоскости, проходящие через начало координат, а линиями тока - окружности. Скорость течения, согласно формуле (29), равна

ds г dip

(48)

Для г = О скорость получается равной бесконечности; поэтому физически такой поток возможен только вне некоторого ядра конечного диаметра (на рис. 61 оно заштриховано). Ядро может быть образовано твердым телом или вращающейся жидкостью (движение которой не является потенциальным), наконец, оно может состоять из другой, более легкой жидкости, не принимающей участия в движении. Примером последнего случая является полый водяной вихрь, в котором вода совершает круговое движение вокруг ядра из воздуха. Под действием силы тяжести свободная поверхность такого полого вихря принимает форму, изображенную на рис. 62. Уравнение этой поверхности получается путем применения уравнения Бернулли к двум линиям тока и имеет вид:

Z - Zo - 1у- - Zo - -- 2g 2gr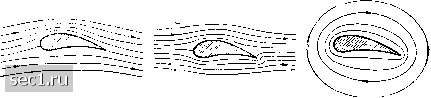

Рис. 63. Поток около кры- Рис. 64. Обычный потен- Рис. 65. Пиркуляцион-ла циальный поток около ный поток вокруг кры-

крыла ла

Подобного рода воронки часто наблюдаются в реках, в ваннах (при спуске воды) и т.д. Во всех таких случаях мы имеем дело с потоками, в которых циркуляция уже существует и вызвана какими-то посторонними причинами.

Другим примером потенциального потока с циркуляцией является поток около крыла самолета (рис. 63). Этот поток получатся из обычного потенциального потока без циркуляции (рис. 64) путем наложения на последний циркуляционного потока, изображеннго на рис. 65, вследствие чего при обтекании крыла также возникает циркуляция. С циркуляцией тесно связано возникновение подъемной силы крыла. Без всякого расчета легко видеть, что при наложении циркуляционного потока на обычный потенциальный поток (рис. 64) скорость последнего над крылом увеличивается, а под крылом, наоборот, уменьшается. Согласно уравнению Бернулли это означает, что над крылом давление уменьшается, а под крылом увеличивается, следовательно, возникает сила, действующая на крыло снизу вверх, т.е. подъемная сила. Кут-та (Kutta) и И. Е. Жуковский независимо друг от друга нашли путем теоретических расчетов, что подъемная сила на единицу длины крыла равна

А = pTV,

где р есть плотность жидкости, Г - циркуляция, а У - относительная скорость крыла и жидкости. Следовательно, подъемная сила прямо пропорциональна циркуляции. Вывод указанной формулы будет дан ниже, в §13.

Если движение начинается из состояния покоя, то, согласно теореме Томсона, в получившемся потоке циркуляция не может возникнуть даже в том случае, когда движение происходит в многосвязной области.

См. по этому поводу сноску на стр. 107.

В самом деле, в состоянии покоя циркуляция вдоль всякой замкнутой кривой равна нулю, поэтому она должна остаться равной нулю и после начала движения. В действительности же циркуляция, как правило, возникает, и причиной этого является образование поверхности раздела. Так, например, в спиральной камере, изображенной на рис. 36, в первый момент начала движения образуется на остром ребре к поверхность раздела, из которой возникает вихрь такого же вида, как на рис. 43. В дальнейшем вихрь отрывается от ребра и уплывает вместе с потоком, но вызванная им циркуляция остается в потоке на все время. Совершенно аналогичная картина наблюдается и при движении крыла. В начале движения поток под крылом огибает заднюю кромку крыла снизу вверх (рис. 64), вследствие чего здесь образуется поверхность раздела, превращающаяся в вихрь (рис. 66). В дальнейшем вихрь отрывается от крыла и уплывает вместе с потоком, но оставляет в нем циркуляцию, равную по абсолютной величине своей циркуляции, но противоположно направленную. При этом вдоль жидких линий, заключающих внутри себя крыло и вихрь вместе, циркуляция остается равной нулю, как этого и требует теорема Томсона.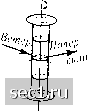

Рис. 66. Вихрь, образующийся при разгоне крыла

Рис. 67. Вращающийся цилиндр

Для того чтобы от присутствия крыла область пространства сделалась двухсвязной, необходимо, чтобы крыло с боков было ограничено двумя параллельными стенками или чтобы крыло простиралось в обе стороны до бесконечности. Для действительных крыльев ни одно из этих условий не соблюдается. Тем не менее циркуляция, без которой не может получиться подъемная сила, возникает и в этом случае. Она возникает вследствие отрыва вихрей, образующихся из поверхности раздела с поперечным скачком скорости (рис. 46). Подробнее об этом будет сказано в § 15 гл. III.

Если на вращающийся круглый цилиндр набегает поток воздуха в направлении, перпендикулярном к оси цилиндра (рис. 67), то вокруг