него возникает циркуляция такого же вида, как и вокруг крыла. В дальнейшем, в § 7 гл. III, мы увидим, что причиной возникновения этой циркуляции является трение. Циркуляция вокруг цилиндра создает силу, действующую на цилиндр в направлении, перпендикулярном к направлению потока, и называемую поэтому поперечной силой. На единицу длины оси цилиндра эта сила равна, как и при циркуляции вокруг крыла, pTV. Такая же сила возникает и при набегании потока на трехгранную или четырехгранную призму, вращающуюся вокруг продольной оси, на вращающийся шар и т. д. Направлена поперечная сила всегда к той стороне вращающегося тела, на которой направление вращения и направление потока совпадают. Возникновение при указанных условиях поперечной силы называется, по имени ученого Магнуса (Magnus), впервые открывшего (в 1852 г.) это явление, эффектом Магнуса.

До изобретения нарезных артиллерийских орудий часто случалось, что шаровые снаряды после вылета из ствола значительно отклонялись в сторону от той траектории, по которой они должны были бы лететь. Магнус показал, что причиной такого поведения снаряда служило вращение вокруг поперечной оси, которое шаровой снаряд получал вследствие случайных причин. На основании сказанного выше это создавало условия, необходимые для возникновения поперечной силы, которая и вызывала нежелательное отклонение снаряда от намеченной траектории. Такие же боковые отклонения, часто очень значительные, наблюдаются и при полете «срезанного» мяча при игре в теннис или гольф. Несколько лет тому назад А. Флеттнер (Flettner) использовал эффект Магнуса для приведения в движение корабля энергией ветра, причем вместо парусов он установил вертикальные быстро вращающиеся цилиндры (роторы). На концах цилиндров помещались выступающие круглые диски (рис. 67), так как иначе воздух, расположенный выше и ниже цилиндра, засасывался в область потока с пониженным давлением и, возмущая поток, уменьшал поперечную силу. Испытания показали техническую пригодность такого роторного корабля, но в экономическом отношении он оказался менее выгодным обычных моторных судов и поэтому не получил дальнейшего применения.

Эффект Магнуса можно продемонстрировать при помощи следующего опыта. Поставим на рельсы легкую тележку с вертикальным цилиндром, приводимым во вращение маленьким электромоторчиком, и начнем обдувать этот цилиндр потоком воздуха, направленным поперек рельсов (для получения такого потока можно воспользоваться настольным вентилятором). Тележка сейчас же начнет двигаться вдоль рельсов. Устанавливая вентилятор так, чтобы поток воздуха набегал

на цилиндр под непрямым углом к направлению рельсов, можно исследовать движение цилиндра-паруса на разных курсах. Можно даже заставить тележку катиться против ветра под острым углом. При перемене направления вращения цилиндра тележка катится в обратную сторону.

Можно произвести также следующий опыт. Приведем в быстрое вращение легкий цилиндр, расположив при этом его ось горизонтально, и предоставим цилиндру падать. Мы увидим, что вместо того, чтобы упасть вертикально вниз, цилиндр начнет планировать по довольно пологой траектории. При таком движении (рис. 68) на цилиндр, кроме подъемной (поперечной) силы А, перпендикулярной к направлению движения, действует еще сопротивление W, направленное против движения, которое, однако, в случае длинного и узкого цилиндра и при наличии боковых дисков значительно меньше, чем подъемная сила. Равнодействующая этих обеих сил уравновешивает вес цилиндра и тем самым замедляет его падение.

Рис. 68. Силы, действующие на падающий вращающийся цилиндр

§ 12. Движение жидкости, лишенной трения, с вращением частиц. Вихревые нити. Для изучения движений однородной, лишенной трения жидкости с вращением частиц воспользуемся опять теоремой Томсона о постоянстве циркуляции по замкнутому жидкому контуру. Из этой теоремы и из геометрических свойств ротации скорости (называемой также вихревым вектором) можно вывести известные теоремы Гельмгольца о вихревых движениях. Эти теоремы, касающиеся весьма важных геометрических и механических соотношений, имеющих место при движении жидкости с вращением частиц, были выведены самим Гельмгольцем несколько иным путем, а именно - на основе электродинамических представлений. Однако следствия, вытекающие из этих теорем, получаются простыми только в том случае, когда частицы жидкости, находящиеся во вращении, занимают область в виде нити, и вне этой области движение происходит без вращения частиц. В таком случае говорят о вихревых нитях. Важнейшие теоремы о вихревых нитях можно вывести из свойств окружающего их потенциального течения, не углубляясь при этом в детали движения жидкости с вращением частиц. Таким образом, мы должны вернуться

Helmholtz Н., Crelles Journ., т. 55 (1858), стр. 25.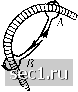

к потенциальному движению с циркуляцией, о котором мы говорили в § 11. Напомним, что область, в которой происходит такое потенциальное движение, является многосвязной и что циркуляция по всем кривым, которые можно перевести друг в друга, не пересекая границ области, одинаковая. Отсюда, как мы сейчас увидим, следует, во-первых, что вихревая нить долж-Рис. 69. Вих- на либо иметь форму кольца, т. е. быть замкнутой, либо ревая нить доходить своими концами до границ жидкости, и, во-вторых, что циркуляция вокруг вихревой нити в один и тот же момент времени во всех местах должна быть одинаковой. В самом деле, проведем в потоке замкнутую линию, состоящую из двух петель А и В вокруг вихревой нити и двух отрезков АВ и В А (рис. 69). Эту линию можно путем непрерывной деформации стянуть в точку, не пересекая вихревой нити. Следовательно, циркуляция вдоль этой линии равна нулю. Но эта циркуляция складывается из четырех частей, две из которых получаются при интегрировании вдоль отрезков АВ и ВА, а две другие - при интегрировании вдоль петель А и В. Циркуляции вдоль примыкающих друг к другу отрезков АВ и В А взаимно уничтожаются, так как эти отрезки при интегрировании обходятся в противоположных направлениях. Следовательно, должны взаимно уничтожаться и циркуляции вдоль петель А и В, так как иначе полная циркуляция по всей жидкой линии не была бы равна нулю. Это означает, что циркуляции вдоль петель А и В равны по абсолютной величине, но противоположны по знаку. Но проведенная замкнутая линия огибает вихревую нить около А и около В в противоположных направлениях, поэтому циркуляция около А и в, взятая в одном и том же направлении, должна быть одинаковая. Если бы вихревая нить оканчивалась где-либо внутри жидкости, то мы могли бы одну из петель снять с вихревой нити, в то время как вторая продолжала бы оставаться на вихревой нити. Тогда первая петля потеряла бы свою циркуляцию, а вторая - сохранила. Следовательно, изменилась бы полная циркуляция вдоль проведенной замкнутой линии при перемещении последней в пределах области потенциального движения, что, однако, невозможно. Таким образом, мы приходим к следующей теореме: Вихревая нить не может оканчиваться нигде внутри жидкости и имеет везде одинаковую циркуляцию. К этому, чисто геометрическому свойству вихревой нити присоединяется еще динамическое свойство, вытекающее из теоремы Томсона: Циркуляция вокруг вихревой нити не изменяется с течением времени.