мени около сечения А равно

И по направлению противоположно скорости wa- Векторную сумму этих изменений количеств движения, отнесенных к единице времени, следует приравнять результирующей всех внешних сил, действующих на выделенную массу жидкости. Вместо изменений количеств движения можно рассматривать соответствующие им «реакции», т.е. силы такой же абсолютной величины, но противоположного направления. Векторная сумма этих реакций, очевидно, уравновешивается внешними силами, приложенными к выделенной массе жидкости. Следовательно, в случае жидкой струйки, изображенной на рис. 73, реакция в сечении А направлена в сторону скорости wa, а в сечении В - в сторону, обратную скорости wb-

Для правильного применения теорем о количестве движения и о моменте количества движения целесообразно ограничивать рассматриваемую массу жидкости замкнутой, так называемой контрольной поверхностью (на следующих ниже рис. 77 и 78 эта поверхность отмечена пунктиром). Векторная сумма всех внешних сил, действующих на жидкость, заключенную внутри контрольной поверхности, должна, согласно сказанному выше, уравновешиваться с векторной суммой реакций, вычисленных для всех жидких струек, проходящих через выделенную область. Следовательно, должны быть равны нулю суммы проекций всех сил и суммы моментов всех сил для всех координатных осей. Однако очень часто можно ограничиться составлением уравнения равновесия только для одного координатного направления.

При неустановившемся движении изменение количества движения выделенной массы жидкости происходит не только вследствие перемещения границ, но и вследствие изменения скоростей внутри выделенной жидкости. Если, как это часто бывает при турбулентных движениях, скорость неустановившегося потока в среднем не изменяется, то сумма изменений количеств движения внутри выделенного объема в среднем получается равной нулю, и тогда можно применять к неустановившимся потокам теоремы о количестве движения и моменте количества движения также, как и к установившимся. Правда, в таких случаях необходимо соблюдать осторожность при составлении средних значений на контрольной поверхности (см. §14).

Рассмотрим несколько примеров применения теорем о количестве движения и моменте количества движения.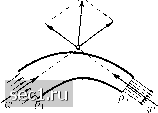

Рис. 74. Движение жидкости в изогнутом канале

а) Сила, с которой жидкость, текущая по изогнутому каналу, действует на его стенки. Пусть жидкость входит в канал со скоростью wi (рис. 74) при давлении pi и выходит из канала со скоростью W2 при давлении р2. Пусть далее, Fl есть площадь входного поперечного сечения, а F2 - площадь выходного поперечного сечения. Тогда изменение количества движения во входном поперечном сечении будет равно pFiw\ и направлено против скорости wi. Этому изменению количества движения соответствует равная по величине, но противоположно направленная сила, с которой текущая жидкость действует на стенки канала. К этой силе прибавляется еще сила давления, равная piFi и направленная в ту же сторону. Следовательно, жидкость, вступающая в канал, действует на его стенки с силой Fi{pw\ -\-pi). Аналогичным образом, жидкость при выходе из канала действует на его стенки с силой F2{pw\ Ч-рз)? направленной против скорости W2, т.е. опять внутрь контрольной поверхности. Геометрическая сумма сил Fi{pwl -\-pi) и F2{pwl -\-Р2) представляет собой полную реакцию жидкости, текущей по изогнутому каналу, на его стенки.

Ь) Реакция вытекающей струи. Пусть струя вытекает через отверстие в стенке из области, давление в которой равно pi, в область, давление в которой равно рг- Количество движения, переносимое струей, равно

J = pF,w\

где W есть скорость истечения струи, а Fg - площадь поперечного сечения струи. Подставляя вместо w его значение согласно формуле (17), мы получим:

J = 2F,{pi -Р2).

Следовательно, количество движения, переносимое струей, равно удвоенной силе давления pi - р2 на площадь поперечного сечения струи, причем направлено оно в сторону скорости истечения. Этому переносу количества движения соответствует реакция вытекающей струи, равная по величине, но противоположно направленная. Удвоенная величина давления объясняется тем, что в отверстии, кроме исчезновения избыточного статического давления Fg{pi -Р2), происходит дополнительное уменьшение давления на такую же величину вследствие притекания

жидкости к отверстию. Реакцию вытекающей струи легко обнаружить, если поместить сосуд, из которого происходит истечение, на легкую тележку. Тогда тележка вместе с сосудом будет двигаться в направлении, противоположном направлению истечения струи. На реакции вытекающей струи основано действие так называемого сегнерова колеса (рис. 75). С помощью такого колеса можно поднимать на высоту груз, как это показано на рис. 75, или выполнять другую работу. В прежние времена сегнеровы колеса строились часто больших размеров.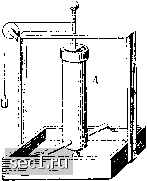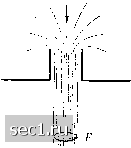

Рис. 75. Колесо Сегнера

Рис. 76. Насадок Борда

В одном частном случае, а именно при истечении через так называемый насадок Борда (рис. 76), теорема о количестве движения позволяет вычислить коэффициент сжатия струи, т. е. отношение поперечного сечения струи Fg к поперечному сечению отверстия F (см. §5). В самом деле, при истечении через насадок Борда на любую часть стенок сосуда действует в направлении истечения струи полное избыточное давление pi - р2 Поэтому количество движения 2Fs{j)i - Р2), переносимое струей, должно уравновешиваться силой давления F{pi - Р2) во входном поперечном сечении, следовательно, должно соблюдаться равенство

F{pi-P2) =2F,(pi -Р2),

откуда находим:

F. = F,

т.е. коэффициент сжатия равен Уз-