перпендикулярная к направлению скорости V. Следовательно, на участок лопатки или крыла длиной / действует сила

A = pTVl.

(56)

Сила А называется поперечной, или подъемной силой. Соотношение, выражаемое уравнением (56), называется теоремой Жуковского о подъемной силе-. Эта теорема может быть доказана также другим путем. Так, например, Н.Е.Жуковский вывел ее, применив теорему о количестве движения к контрольной поверхности в виде круглого цилиндра очень большого радиуса и с осью, совпадающей с осью крыла. При этом одна половина подъемной силы А получается вследствие переноса количества движения, а другая половина как результирующая сил давления. Теорема Жуковского важна прежде всего потому, что она дает возможность вычислить по заданной подъемной силе соответствующую циркуляцию, определяющую напряженность вихря позади крыла.

/) Уравнение Эйлера для турбины. Пусть в рабочее колесо турбины (рис. 79) на расстоянии Гх от центра колеса вступает поток воды, абсолютная скорость которого в точке входа равна v)i, а направление образует с направлением движения колеса угол масса воды, протекающая в одну секунду, пусть равна М. Внутри колеса вода движется в направлении, приближенно совпадающем с направлением лопаток. На расстоянии Г2 от центра колеса вода стекает с лопатки, имея абсолютную скорость v)2, направление которой образует с направлением движения колеса угол /З2.

Абсолютная скорость v)2 получается векторным сложением скорости движения воды вдоль лопатки и окружной скорости той точки лопатки, в которой вода покидает колесо. Применяя к этому движению теорему о моменте количества движения, мы получим независимо от того, что происходит внутри колеса, следующее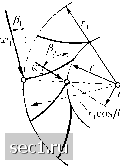

-2COS/?2

Рис. 79. К выводу теоремы Эйлера о турбине

соотношение:

Ш = M{wiri cos/3i - W2r2 COS/32),

Автор неправильно называет соотношение (56) теоремой Кутта - Жуковского. В действительности эта теорема впервые была установлена Н. Е. Жуковским в 1904 г., и поэтому здесь и в дальнейшем она нами называется теоремой Жуковского. (Прим. перев.)

называемое уравнением Эйлера для турбины. Из этого уравнения видно, что вращающий момент, передаваемый водой на турбину, будет наибольшим, следовательно, условия работ турбины будут наивыгоднейшими в том случае, когда cos /З2 = О, т. е. когда вода покидает лопатку в радиальном направлении (очевидно, что в этом случае потеря кинетической энергии водой, выходящей из колеса, будет наименьшей). Умножая вращающий момент на угловую скорость вращения uj, мы получим мощность. Для указанного наивыгоднейшего случая она равна

L = Ши) = Mnujwi cos/3i.

Применяя уравнение Эйлера к потоку жидкости в неподвижной спиральной камере с отверстием в середине (§6), мы получим:

Ш = М(ы)1Г1 C0S/3l - ы)2Г2 cos/32) = О,

откуда

ТО1Г1 C0S/3l = TO2r2 соз/Зг,

где через /3 обозначены углы, образуемые скоростью потока с направлением, перпендикулярным к отрезку, соединяющему центр отверстия с рассматриваемой точкой потока. Если все углы /3 достаточно малы, следовательно, можно принять, что C0S/3 = 1, то мы получим:

wr = const,

т. е. тот же результат, который мы нащли в § 6 иным путем.

§ 14. Теорема о количестве движения для потоков с пульсациями скорости. Среди неустановившихся течений часто встречаются такие, в которых скорость в каждой точке пространства хотя и изменяется со временем, причем иногда даже значительно и очень неравномерно, тем не менее в среднем она остается постоянной для любого достаточно большого промежутка времени. Совокупность таких средних значений скорости во всех точках пространства определяет собой некоторое установившееся течение. Действительное, т.е. неустановившееся, течение в таких случаях принято называть течением, в среднем установившимся. Простой случай такого течения мы рассмотрели в примере с) предыдущего параграфа.

Обозначим для течения, в среднем установившегося, средние значения составляющих скорости вдоль осей координат через й, U, w, а мгновенные отклонения составляющих фактической скорости и, v, V), от соответствующих средних значений - через и, v и w. Тогда мы будем иметь:

и = 11 +и, v = v + v, w = w + w,

ри dt,

где интеграл представляет собой изменение количества движения в течение более или менее длительного промежутка времени Т. Обозначая для краткости среднее значение чертой над буквой, мы можем написать:

Мы имеем:

ри dt = ри". и2 = (й + и) = м+2йи+и.

Для того чтобы вычислить среднее значение от и , учтем, что среднее значение от равно опять й, так как й уже является средним значением от и. Среднее значение от и равно, согласно определению, нулю. Среднее значение от и не может быть равно нулю, так как все величины и положительны. Следовательно,

pu=pW+pu. (57)

Таким образом, в рассматриваемом случае к количеству движения рй течения, в среднем установившегося, надо прибавить количество движения ри, являющееся средним значением количеств движения пульсации и. Если вместо количеств движения рассматривать соответствующие им реакции, то количеству движения ри будет соответствовать.

причем, согласно определению, средние значения величин и, v, w, называемых пульсациями скорости, или пульсационными скоростями, равны нулю.

Применяя теорему о количестве движения к течениям, в среднем установившимся,нельзя оперировать только со средней скоростью. Необходимо, как мы сейчас увидим, учитывать также пульсации скорости, составляя для этого средние значения всех количеств движения, переносимых через неподвижную контрольную поверхность.

Вычислим сначала составляющую количества движения вдоль оси X для участка контрольной поверхности, перпендикулярного к оси X. В промежуток времени dt через единицу площади контрольной поверхности проходит масса р и dt; она переносит с собой количество движения pvdt. Изменение количества движения за одну секунду равно