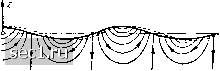Рис. 81. Линии тока волнового движения

Точная теория показывает, что формула (62) справедлива только для низких волн, причем независимо от их высоты. Для высоких волн скорость с в действительности несколько больше того значения, которое дает формула (62). Кроме того, при высоких волнах траектории частиц воды, расположенных на свободной поверхности, получаются незамкнутыми: вода на гребне волны уходит вперед на большее расстояние, чем на то, на которое она возвращается назад во впадине волны (см. правую часть рис. 81). Следовательно, при высоких волнах происходит перенос воды вперед.

Для волн с небольшой длиной важным фактором является, кроме силы тяжести, также поверхностное натяжение. Оно стремится сгладить волновую поверхность, и поэтому скорость распространения волн увеличивается. Теория показывает, что в этом случае скорость распространения волн равна

27Г рА

(63)

где С есть капиллярная постоянная. Для длинных волн преобладающую роль играет первый член под знаком корня, а для коротких волн, наоборот, второй член. Для длины волны

"с

Л: =2../

скорость распространения с имеет минимальное значение, равное

Cl =

Для воды р = 1, С = 72, 5 дин/см, следовательно,

Al = 1,72сж, Cl = 23,3см/сек.

Волны, длина которых больше Ai, называются гравитационными, а волны, длина которых меньше Ai, - капиллярными.

От скорости перемещения гребней волн, называемой фазовой скоростью (выше мы ее называли скоростью распространения волн и обозначали через с), следует отличать скорость распространения группы

есть длина волны, а величина

Щ-=Т (65)

есть период колебаний. Если

цх - vt = const,

т.е. если

X = const + t,

то аргумент синуса не зависит от времени, поэтому не зависит от времени и ордината у. Это означает, что вся волна, не изменяя своей формы, перемещается вправо со скоростью

с=. (66)

Наложим на эту волну вторую волну

у = А sm(p.x - ut),

т. е. волну с той же амплитудой А, но с несколько иными значениями иг/. Результирующим движением будет

у + у = A[sin{p.x - ut) + sin{p!x - ft)].

В тех точках оси ж, в которых фазы обоих колебаний совпадают, амплитуда равна 2А, в тех же точках, в которых фазы обоих колебаний

волн, называемую групповой скоростью и обозначаемую через с*. Проще всего разъяснить смысл этого понятия на примере движения, возникающего в результате наложения двух волн, имеющих равные амплитуды, но немного отличающихся своей длиной. Пусть мы имеем синусоидальную волну

у = Asin{iix - vt), где А есть амплитуда, t - время, а рь vi и - некоторые коэффициен-

тт 27Г . 27Г

ты. При увеличении х па - или t па - синус принимает прежнее значение, следовательно, величина

f = А (64)

В этом равенстве член

sm -X-X---t

представляет собой волну, для которой коэффициенты при х vi t равны средним значениям от и и соответственно от г/ и и. Множитель

2Лсо8 „ж---i

Рис. 82. Биение который при малых значениях раз-

ностей ц - ц и v - v изменяется медленно, можно рассматривать как переменную амплитуду (рис. 82). Группа волн кончается в той точке, где косинус делается равным нулю. Скорость перемещения этой точки, называемая групповой скоростью с*, на основании соображений, аналогичных предыдущим, равна

. у - у ~ г

р- р

Для длинных групп, т.е. для медленных биений, с достаточной точностью можно принять, что

с* = -. dp

Для волн, возникающих под действием силы тяжести, из формулы (60) мы имеем:

Но, согласно равенству (65),

противоположны, амплитуда равна нулю. Такое явление называется биением. Применив известную формулу

• а „ . а + /3 а-/3 sm а + sm /5 = 2 sm --- cos --

мы получим:

у + у = 2А sin - А cos -