=\lb = \lfi. (68)

поэтому

г/ = /gfl.

Отсюда, диференцируя по р. и имея в виду равенство (67), мы найдем:

Таким образом, группы волн распространяются со скоростью с*, равной половине фазовой скорости, иными словами, гребни в группе волн перемещаются со скоростью, в два раза большей, чем сама группа волн; на заднем конце группы все время возникают новые волны, а на переднем конце группы они исчезают. Это явление очень легко наблюдать на волнах, вызванных падением камня в неподвижную воду.

Все сказанное относится не только к волнам на поверхности воды, но и к любым другим волнам, фазовая скорость которых зависит от длины волны.

Другим видом групп волн являются волны, возникающие на поверхности воды при движении корабля. Картину волн, очень похожую на корабельные волны, легко получить, если на поверхности покоящейся глубокой воды заставить двигаться с постоянной скоростью точечный очаг возмущения давления. Возникающее при этом движение может быть исследовано математически. Согласно вычислениям В. Томсона (lord Kelvin), Экмана (Ekman) и других, получается система волн, изображенная на рис. 83, на котором наклонными линиями обозначены гребни волн. Эта система волн перемещается вместе с очагом возмущения. Длина поперечных волн на основании формулы (62) равна

, 27гс2

где с есть скорость перемещения очага возмущения. При движении корабля образуются две системы таких волн - одна около носа, другая около кормы корабля, причем волны обеих систем интерферируют друг с другом.

следовательно,

С другой стороны, подставив в формулу (62) значение Л из равенства (64), мы получим: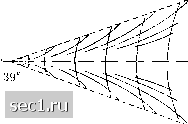

Групповая скорость капиллярных волн, как нетрудно показать путем расчета, аналогичного сделанному для гравитационных волн, больше фазовой скорости, а именно, в предельном случае очень малых волн, в 1,5 раза. Следовательно, если очаг возмущения движется с постоянной скоростью, то группы волн его опережают. Около лески удочки, опущенной в реку, скорость течения которой больше 23,3 см/сещ образуются вверх по течению капиллярные волны, а вниз по течению - гравитационные волны, причем последние имеют приблизительно такую же форму, как на рис. 83, а первые расходятся вверх по течению в виде дуг окружностей. При скоростях движения очага возмущения, меньших 23,3 см/сек, волны не образуются.

На поверхности соприкосновения двух жидкостей различной плотности, расположенных одна над другой, также могут возникать волны. Если обе жидкости неподвижны и плотности их равны рх и рг, то теоретический расчет дает для фазовой скорости волн величину

Рис. 83. Система волн, образующихся при равномерном движении на поверхности воды очага возмущения давления

/gApi - р2 2туС

У21ГР1+Р2 Х(р+р2у

(70)

Если верхняя жидкость течет со скоростью wi относительно нижней, то теория показывает, что возникающие волны устойчивы только в том случае, если их длина достаточно велика. Короткие же волны, подобно тому, как это было показано в § 7 для движения двух потоков жидкости вдоль поверхности раздела, неустойчивы, что приводит к перемешиванию обеих жидкостей в промежуточной зоне; это перемешивание восстанавливает устойчивость течения. При увеличении скорости v)i граница между неустойчивостью и устойчивостью перемещается в сторону волн с большей длиной. Волны такого рода могут возникать также в атмосфере на границе двух слоев воздуха разной плотности, движущихся относительно друг друга; иногда эти волны делаются видимыми благодаря образованию так называемых волнистых облаков.

При движении воздуха над поверхностью воды также образуются волны. Однако теория таких волн, основанная на предположении отсутствия трения, приводит к результатам, противоречащим действи-

iTomson W., Phil. Mag. (4), т. 42 (1871), стр. 368.

Jeffreys Н., Proc. Roy. Soc. (А),т. 107 (1925), стр. 189, и т. 110 (1926), стр. 241. Motzfeld Н., ZAMM, т. 17, (1937), стр. 193-212.

тельности. Так, например, вычисления В. Томсона показали, что минимальная скорость ветра, необходимая для образования на поверхности воды волн, должна составлять круглым числом 6,4 м/сек, причем возникают волны, обладающие минимальной скоростью распространения с = 23,3 см/сек и длиной волны А = 1,72 см (при большей скорости ветра получаются, конечно, волны с большей длиной). Между тем в действительности для образования волн достаточно ветра со скоростью 1 м/сек. Согласно исследованию Джеффри это объясняется тем, что вследствие трения распределение давления на поверхности волны делается несимметричным, и поэтому ветер, если его скорость больше фазовой скорости волн, совершает на гребне каждой волны работу. Мотцфельд, измерив распределение давления на поверхности моделей водяных волн, нашел, что сопротивление, которое воздух оказывает движению волн, пропорционально полуторной степени наклона поверхности волны в точке перегиба относительно горизонта, а также квадрату разности между скоростью ветра wb и фазовой скоростью волн. Далее, Мотцфельд путем расчета нашел, что наклон поверхности волны в точке перегиба, зависящий от фазовой скорости с, получается наибольшим при

с = wb.

Этой скорости с соответствует, на основании формулы (62), волна длиной

Если принять во внимание поверхностное натяжение, которое Мотцфельд не учитывал, то расчет показывает, что для возникновения легкого волнения на поверхности воды достаточно, в полном соответствии с наблюдениями, ветра со скоростью, немного превышающей 23,3 см/сек.

Формулы, выведенные выше, пригодны только для волн на глубокой воде. Они еще достаточно точны, если глубина воды равна половине длины волны. При меньшей глубине частицы воды на поверхности волны описывают не круговые траектории, а эллиптические, и зависимость между длиной и скоростью распространения волн получается более сложной, чем для волн на глубокой воде. Однако для волн на