плотиной или на некотором расстоянии перед ней возникает вал конечной высоты, так называемый прыжок воды, причем этот вал ни в какой мере не влияет на движение воды до плотины. В § 2 и 4 гл. IV мы увидим, что сходное явление происходит и при движении газовых потоков, причем там роль критической скорости л/gh играет скорость звука. Движение воды в открытом русле со скоростью, меньшей \/gh, называют спокойным течением, а движение со скоростью, большей \/gh, - стремительным течением.

Вычислим для заданного расхода воды Q (на единицу ширины русла) значения глубины, соответствующие возрастающим скоростям течения w (рис. 85). Понижение уровня в каком-нибудь сечении относительно уровня неподвижной воды равно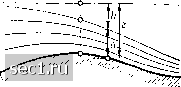

Рис. 85. Перетекание воды через плотину

Глубина воды в этом сечении, обеспечивающая при скорости w расход Q, очевидно, равна

Следовательно, расстояние соответствующей точки дна от уровня неподвижной воды будет

(75)

При изменении скорости w от О до оо величина z изменяется от оо до оо, принимая в промежутке конечные значения; поэтому при определенном W она должна иметь минимальное значение (в § 3 гл. IV мы увидим, что таким же образом изменяется поперечное сечение трубки тока при движении газа). Взяв производную от правой части уравнения (75) и приравняв ее нулю, мы найдем, что указанный минимум имеет место при скорости

wi = VQg-

Этой скорости соответствуют значения h и а, равные

ai =

= 2hi.

Отсюда следует, что

wi = л/gal,

т.е. скорость wi равна скорости распространения вала на воде с глубиной ai. Произведенный расчет показывает, что при перетекании воды через пологое возвышение на дне глубина воды над наивысшей точкой возвышения равна % расстояния z этой точки от уровня неподвижной воды. Скорость течения воды над этой точкой равна

следовательно, расход Q равен

Q = aw=lzJlgz.

(76)

Ниже вершины возвышения течение воды стремительное, но затем оно опять делается спокойным, причем переход в спокойное течение происходит обычно резко - путем образования прыжка воды (см. ниже).

Для непологих возвышений

~ ------нельзя принимать, что скорость

течения одинакова во всем поперечном сечении, однако в качественном отношении результаты остаются такими же, как и в рассмотренном случае [ср. с § 12, п. е) следующей главы].

Выведенные формулы могут быть использованы также в более широких целях. Рассмотрим русло, на дне которого имеется пологое возвышение (рис. 86), и для ряда высот уровня неподвижной воды (штрих-пунктирные прямые) вычислим и отложим на рисунке глубины а при определенном значении секундного расхода Q (для каждой точки дна русла и каждой высоты уровня мы получим два значения глубины а). Найденные таким путем профили свободной поверхности воды изображены на рис. 86. Наинизшему возможному положению уровня неподвижной воды соответствует профиль I-IV, проходящий через двойную точку. Для течения, изображенного на рис. 85, возможен только этот профиль. Профили I-II и III-IV, соответствующие более высоким уровням неподвижной воды, также встречаются в практических

Рис. 86. Профили свободной поверхности воды при перетекании через возвышение на дне русла

Рис. 87. Профиль свободной поверхности воды при перетекании через возвышение на дне русла. Скорость течения мень-

ше критической скорости

Рис. 88. Профиль свободной поверхности воды при перетекании через возвышение на дне русла. Скорость течения больше критической скорости -/gh

Рис. 89. Профиль свободной поверхности воды при перетекании через возвышение на дне русла с образованием прыжка. До прыжка скорость течения больше, а после прыжка меньше -/gh

условиях (рис. 87 и 88). Профили П-IV, изображенные на рис. 86 штрихами и построенные для уровней неподвижной воды, более низких, чем наименьший возможный, практически осуществляются только в своей верхней части после прыжка воды, связанного с потерей энергии (рис. 89).

Скорость течения, изображенного на рис. 87, меньше критической скорости \/gh, и над вершиной возвышения дна получается понижение уровня воды. Наоборот, для случая, изображенного на рис. 88, скорость течения больше критической скорости \/gh, и уровень воды над возвышением дна поднимается, причем на высоту, большую высоты возвышения. Наконец, для случая, изображенного на рис. 89, скорость течения на участке от возвышения дна до прыжка больше, а после прыжка меньше критической скорости л/gh.

О роли, которую в рассмотренных явлениях играет трение, будет сказано в § 12, п. /) гл. III.

Еще раз подчеркнем, что в предыдущих рассуждениях мы пренебрегали влиянием вертикального ускорения. Учет этого ускорения при стремительном течении приводит только к незначительным количественным поправкам; при спокойном же течении получается качественное изменение характера движения: вниз по течению от очага возмущения возникают волны.

Boussinesq J., Essai sur la theorie des eaux courantes. Mem. des Savants Ertrang., T. 23 (1877); см. также Fo г с h h e i m e г Ph., Hydraulik, изд. 3, 1930 [имеется в переводе на русский язык: Форхгеймер Ф., Гидравлика, Москва, 1935 (Прим. перев.)