Tollmien W., Ein allgemeines Kriterium der Instabilitat laminarer Geschwindigkeitsverteilungen. Gottinger, Nachr., Math.-Phys. Klasse, Fachgruppe I, T. I (1935), стр. 79.

Cm. равенство (17), из которого видно, что направление, в котором давление

увеличивается, зависит от знака --.

Большие успехи в деле изучения турбулентности были достигнуты в СССР благодаря работам А. Н. Колмогорова, М.Д. Миллионщикова, A.M. Обухова и других; см., например: Колмогоров А.Н., Локальная структура турбулентности в несжимаемой вязкой жидкости при очень больших числах Рейнольдса. Доклады Акад. Наук СССР, т. XXX (1941), №4; Колмогоров А. Н., Вырождение изотропной турбулентности в несжимаемой вязкой жидкости. Доклады Акад. Наук СССР, т. XXXI (1941); Миллионщиков М. Д., Вырождение однородной изотропной турбулентности в вязкой несжимаемой жидкости. Доклады Акад. Наук СССР, т. XXII (1939), №5; Обухов А. М., О распределении масштаба турбулентности в потоках произвольного сечения. Прикл. мат. и мех., т. VI (1942), №2-3; Минский Е. М., О пульсациях скорости при вполне установившемся течении. Журнал техн. физ., 1940, вып. 19; Ландау Л., К проблеме турбулентности. Доклады Акад.

совпадает с наблюденным значением, однако найденное волновое возмущение, имеющее очень большую длину волны, нельзя рассматривать как турбулентность. Настоящая турбулентность, по-видимому, возникает тогда, когда вследствие каких-либо причин, например, вследствие начальных возмущений, в потоке образуются такие распределения скоростей, которые, подобно поверхностям раздела (см. §7 гл. П), неустойчивы и приводят к появлению многих маленьких вихрей. Согласно последним работам Толмина для возникновения неустойчивости достаточно, чтобы профиль скоростей имел точку перегиба, при условии, что число Рейнольдса где 5 есть толщина пограничного слоя, достаточно велико, и притом тем больше, чем круче происходит перегиб профиля. Такие профили скоростей действительно получаются в потоках, в которых давление в направлении движения возрастает. Следовательно, такое возрастание давления действует как фактор, обусловливающий возникновение турбулентности.

Наблюдения показывают, что турбулентность, возникшая вследствие какого-нибудь возмущения, начинает сама собой развиваться дальше вниз по течению. Это ясно видно на снимках, изображенных на рис. 94 и полученных при помощи кинокамеры, двигавшейся параллельно потоку со скоростью продвижения вихрей. Для получения первоначального возмущения было произведено кратковременное отсасывание жидкости через отверстие в стенке (слева, на первом - верхнем снимке). Процесс развития турбулентности до сих пор не получил объ-

Рис. 94. Распространение турбулентности

d) Что касается состояния течения, при котором турбулентность уже вполне развилась, то по этому поводу ограничимся здесь следующими замечаниями.

В § 14 предыдущей главы было показано, что при течениях пульсациями скорости перенос количеств движения, вызванный пульсациями, создает дополнительные напряжения, например, касательное напряжение

(21)

т = -puv,

где и и v суть пульсационные скорости, т. е. отклонения составляющих скорости и и v от их средних во времени значений йий. Для того чтобы сделать формулу (21) пригодной для практических вычислений, необходимо заменить в ней пульсационные скорости какими-нибудь другими величинами, связанными с распределением средней скорости. Для этого следует ввести в расчет определенную длину, которую можно понимать либо как диаметр шарообразного скопления частиц жидкости, движущихся как одно целое, либо как путь, который этот шар должен пройти относительно остальной жидкости, чтобы в результате смешения с окружающим турбулентным потоком потерять свою индивидуальность. Заранее нельзя сказать, что обе эти длины в точности равны друг другу, однако можно предполагать, что между ними существует

Наук СССР, т. XLIV (1944), №8. (Прим. пер.)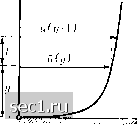

Рис. 95. К выводу формулы для дополнительного касательного напряжения

определенная пропорциональность. Рассмотрим поток, в котором скорость изменяется в направлении, перпендикулярном к линиям тока.

Пусть некоторая масса жидкости из слоя, находящегося от стенки на расстоянии у, перемещается перпендикулярно к направлению потока в слой, находящийся от стенки на расстоянии у -\- I (рис. 95). Если в первом слое средняя скорость течения равна й(у), то вследствие такого перемещения массы жидкости в новое место ее скорость изменится на величину й{у й{у), которую в первом

приближении можно считать равной 1, т.е.

и{у + 1) - и{у) = I

ди ду

Эту величину можно рассматривать, если не равной, то по крайней мере пропорциональной пульсационной скорости и. Что касается пуль-сационной скорости v, то для ее оценки предположим, что два жидких шара, попадающих в рассматриваемый слой с разных сторон и движущихся в этом слое друг за другом, сближаются или удаляются друг от

друга с относительной скоростью 2/. Из этого предположения следует, что пульсационная скорость также должна иметь порядок вели-

чины Наконец, приступая к составлению среднего значения uv, ay

необходимо установить, какие знаки имеют перемножаемые пары значений и и v. Частицы жидкости, переходящие через контрольную поверхность, параллельную стенке, снизу вверх (от стенки), увеличивают свою скорость; наоборот, частицы жидкости, переходящие эту поверхность сверху вниз, уменьшают свою скорость. Отсюда следует, что положительным пульсациям v соответствуют отрицательные пульсации и, а отрицательным v - положительные и, поэтому в обоих случаях произведение uv получается отрицательным. Таким образом, дополнительное напряжение т имеет положительный знак и порядок

величины р{щ Примем неизвестный коэффициент пропорциональности равным единице; такой произвольный выбор этого коэффициента отразится на наших результатах только тем, что величина / останется