Рис. 96. Центральные линии тока расширяющейся струи воздуха

Такая связь между Ь и mi очень хорошо согласуется с формулой (22), выведенной в предыдущем параграфе для дополнительного касательного напряжения. В самом деле, исходя из этой формулы, можно не только вывести найденную связь между 6 и и1, но и вычислить распределение скоростей, причем остается произвольной только постоянная а или какая-нибудь другая, аналогичная постоянной а. Такого рода вычисление было выполнено Толмином". Таким образом, описанное выше поведение расширяющейся струи служит доказательством допустимости применения формулы (22). Не приводя вычислений Толмина, покажем, как можно получить из формулы (22) связь между b и щ путем приближенных оценок.

Как и выше, примем, что I = аЪ. Из теоремы о количестве движения мы имеем:

uib = const = С. Полагая приближенно, что

ди <)Ё1. ду Ь

и подставляя это значение в формулу (22), мы получим среднее значение дополнительного касательного напряжения по поперечному сечению струи:

Сила на единицу объема равна, согласно равенству (6), Напряжение т

изменяется от нуля в середине струи до максимума на некотором расстоянии от середины, а затем уменьшается вновь до нуля, следовательно, произ-

водная сначала отрицательна, а затем положительна. В первой области ду

происходит замедление главного течения, а во второй области - ускорение увлекаемого струей внешнего воздуха. Для центральной части потока можно принять, что

дт о-т

Следовательно, применяя к единице объема этого потока уравнение: масса, умноженная на ускорение, равна силе, мы получим:

2 2

а и{

Tollmien W., Berechnung turbulenter Ausbreitungsvorgange, ZAMM, т. 6 (1926), стр. 468.

В левой части этого уравнения мы можем заменить и на mi; тогда мы получим

Подставляя сюда

dx Ъ

(на основании теоремы о количестве движения) и

мы найдем:

следовательно,

db 02 dx

что хорошо согласуется с экспериментальными результатами, согласно которым Ь = .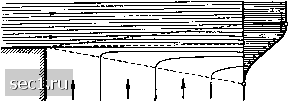

Рис. 97. Размыв края струи

Другим не менее важным случаем, когда можно дать оценку для длины пути перемешивания, является размыв края параллельной струи (рис. 97). В этом случае Ui = const. По-прежнему полагая, что / = аЪ, мы получим для среднего касательного напряжения значение

~ ри\ = const.

Потеря количества движения струи (на единицу толщины потока в направлении, перпендикулярном к плоскости рисунка) пропорциональна ри\Ь, а соответствующее сопротивление W (также на единицу толщины потока в том же направлении) пропорционально ТтХ- Следовательно, как и в предыдущем случае,

Ь ~ ах.

Если струя не выбрасывается, а, наоборот, всасывается из пространства, в котором жидкость неподвижна, то вместо потери количества движения будет иметь место равное по величине приращение количества движения. Практически важно знать наклон края невозмущенной части струи к границе возмущенной области; его можно принять равным 1 : 10.

Ь) При движении жидкости вдоль стенки длина пути перемешивания при приближении к стенке должна стремиться к нулю; это следует непосредственно из самого определения понятия длины пути перемешивания. Отсюда вытекает, что величина внутри потока очень мала,

но вблизи стенки принимает большие значения. На рис. 98 показано распределение скоростей при турбулентном течении, а на рис. 99 - для сравнения - при ламинарном течении.

Рис. 98. Распределение скоростей по поперечному сечению трубы при турбулентном течении

Рис. 99. Распределение скоростей по поперечному сечению трубы при ламинарном течении

Ближайший к стенке слой жидкости прилипает к ней также при турбулентном течении; поэтому вблизи нее сначала образуется тонкий слой, в котором жидкость движется ламинарно, причем так, что при гладких стенках имеет место равенство

Этoт, а также другие случаи рассмотрены у Толмина [Tollmien W., Berechnung turbulenter Ausbreitungsvorgange, ZAMM, т. 6 (1926), стр. 468]; см. также Prandtl L., Uber die ausgebildete Turbulenz. Verb. d. 2 internat. Kongr. f. techn. Mech. (1926), Zurich 1927, стр. 62. Рейхардт в своей работе [VDI-Forschungsheft №414 (1942)] ставит перед собой задачу вычислить все важнейшие факторы, определяющие турбулентное движение, из результатов опыта и выполняет ее на основе собственных измерении для случая свободной турбулентности. Полученная таким образом теория свободной турбулентности изложена в ZAMM, т. 21 (1941), стр. 257. Другая предпосылка для развития теории турбулентности предложена Прандтлем и проверена на некоторых примерах Гертлером [Gortler Н., ZAMM, т. 22 (1942), стр. 241 и 244].