и{у) = (I) , (69)

Blasius, Forschungsarbeiten des Ver. Deutsch. Ing., 1913, №131.

Напоминаем, что при составлении числа Рейнольдса для движений в трубах можно пользоватьзя в качестве характерной длины радиусом, диаметром и гидравлическим радиусом. В соответствии с принятой в этой книге установкой на инженерные расчеты мы пользуемся диаметром.

Lees, Phil. Trans. Roy. Soc. London (A) т.214 (1914), стр. 199; Ргос. Roy. Soc. London (A), T.91 (1915), стр. 40.

"Jakob und Erk, Forschungsarbeiten des Ver. Deutsch. Ing. 1924, №267.

Hermann R., Диссертация, Leipzig, 1930.

ву.Кагтап, ZAMM., т. 1 (1921), стр. 233.

Турбулентное течение в гладких трубах служило предметом многочисленных опытных исследований, некоторые из которых выполнены с очень большой точностью. Относительно такого течения с точки зрения теории можно заранее утверждать только то, что коэффициент сопротивления Л имеет одинаковое значение во всех случаях, когда остается постоянным число Рейнольдса R = § 2. Следовательно, Л может быть функцией только от R. В самом деле, наблюдения показывают, что при увеличении R коэффициент сопротивления Л, уменьшается. Блази-ус в результате обработки опытов Сафа (Saph) и Шодера (Schoder) показал, что примерно до R = 80 ООО, можно принять следующую зависимость между Л и R:

=-R- (

Несколько позже Лис, обработав опыты Стантона (Stanton) и Паннела (Pannel), а также Якоб и Эрк на основе собственных опытов нашли, что зависимость между Л и R вплоть до R = 400 ООО лучше передается формулой

= 00072+g. (67)

В дальнейшем Герман провел опыты почти до числа Рейнольдса R = 2 • 10* и получил формулу:

Л = 0,0054+ (68)

К теоретическому изучению проблемы сопротивления при движении в трубах впервые удалось подойти Карману. Исходя из соображений о подобии, он установил, что имеет место следующее соотношение:

12 10

т.е. разность между наибольшей скоростью в середине трубы и скоростью на расстоянии у от стенки равна динамической

скорости г>* = Yумноженной на некоторую универсальную функцию от отношения . Это соотношение одинаково применимо и к гладким, и к шероховатым трубам, однако вполне строго только для очень больших чисел Рейнольдса, т.е. для случая, когда вязкостью можно пренебрегать. Карман теоретически вы-1,0 вел для функции / формулу, которая дает хорошее совпадение с опытом. В этой формуле только один коэффициент, именно коэффициент к , упоминавшийся уже в § 5, должен быть определен из опыта.

На рис. 127 изображен график функции / iyf, построенный на основании результатов опыта. Пользуясь рис. 127 и уравнением (69), легко вывести формулу для средней скорости w:

О 0,2 0,4 0,6 0,i

Рис. 127. График

тах и

функции построенный на основании результатов опыта

W = Итах - 4,07г!.. dp

(70)

Имея в виду, что падение давления - можно выразить через т = pvl,

а Итах; на основании формулы (70), - через w, мы можем из уравнения (69) и из одного из уравнений (28), (29) и (33) вывести соотношение

между Л = 5 и R = для гладких и шероховатых труб. Не приводя

здесь вычислений, укажем лишь окончательные результаты. Для гладких труб, если взять в основу уравнение (28), получается соотношение:

= 2,01g(R\/A)-0,8,

(71)

практически применимое для всех чисел Рейнольдса в турбулентной области.

Эти вычисления можно найти, например, у Prandtl- Betz, Ergebn. d. AVA, т. 4 (1932), или у Durend, Aerodynamik Theory, т. Ill; см. также Prandtl, VDI-Zeitschr., т. 77 (1933), стр. 109.

Если же взять в основу уравнение (29), то получается более точное для больших R соотношение:

= l,951g(R\/A) -0,55. VA

(72)

В обоих уравнениях (71) и (72) Л входит и в левую, и в правую части. Однако это обстоятельство не вносит каких-либо трудностей в вычисление Л. В самом деле, достаточно в правую часть подставить какое-нибудь предположительно верное значение Л, а затем, в случае необходимости, повторить вычисление еще раз.

Для шероховатых труб, если взять за основу уравнение (33) и для Сг принять значение 8, 5 (шероховатость, создаваемая зернами песка), то при течении, когда шероховатость проявляет себя в полной мере, получается следующее соотношение:

i = 2,0,4 = 1,74.

(73)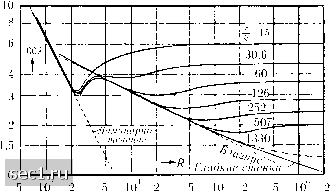

Рис. 128. Зависимость коэффициента сопротивления Л от числа Рейнольдса (сплощные кривые - по измерениям Никурадзе, щтрихпунктирная кривая - по измерениям Бауэра и Галавича)

На рис. 128 зависимость А от числа Рейнольдса для гладких и шероховатых труб изображена в логарифмическом масштабе. Кривые для шероховатых труб (вплоть до самой нижней) получены, путем изме-