инжектор, в котором пар, вытекающий из котла, засасывает холодную воду из колодца и перекачивает ее в котел (действие инжектора объясняется увеличением плотности пара при его конденсации в воду; из котла берется большой объем пара, а взамен него подается значительно меньший объем воды). Мы не можем здесь более подробно заниматься теорией струйных приборов; упомянем только, что в основе этой теории лежат такие же соотношения, как и для дроссельной шайбы и трубки Вентури.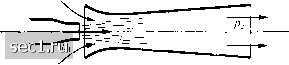

Рис. 134. Струйный насос

Рис. 135. Водослив через плотину с острой вершиной

Рис. 136. Истечение через узкую щель

е) В открытых руслах водослив через плотину (рис. 135) позволяет легко измерить расход воды. Для оценки расхода воды, поскольку речь идет о структуре формулы, можно воспользоваться формулой (75), выведенной в § 16 предыдущей главы. Такую же формулу можно получить из решения совсем другой задачи, на первый взгляд имеющей лишь отдаленное отношение к водосливу. Рассмотрим истечение через узкую вертикальную щель в стенке открытого бассейна (рис. 136). В этом случае можно разбить поперечное сечение щели на узкие элементы bdh. Через каждый такой элемент вытекает количество жидкости

dQ = abdh/2gh.

Интегрируя от О до /ii, мы получим полный расход:

Q=1abhtg.

Эта формула совпадает с формулой (75) принять, что

J V3

i 16 предыдущей главы, если

и заменить hi на z. Такое формальное совпадение обеих формул связано с тем, что размеры, определяющие водослив, из соображений размерности никаким иным образом не могут войти в формулу (77). Более того, опыт показывает, что для вертикального водослива через плотину с острой вершиной (рис. 135) и через щель, изображенную на рис. 136, числовые коэффициенты в формулах для расхода почти совпадают. Особенно тщательные измерения выполнены для водосливов между параллельными стенками (без бокового сжатия струи) через вертикальную плотину с острой вершиной и с доступом воздуха под падающую струю. Согласно Рэбоку,

а = 0,605-Ь

3(/ii - h

0,08/ii

где а есть высота вершины плотины над основанием бассейна, h - небольшая высота, равная 2,85 мм и, по-видимому, связанная с поверхностным натяжением, а hi - высота водослива, т. е. высота над вершиной плотины уровня свободной поверхности воды, измеренная на некотором расстоянии от плотины. Измерение уровня воды производится с хорошей точностью, например, при помощи прибора, изображенного на рис. 137. Острие, фиксирующее уровень воды, обращено кверху потому, что гораздо легче заметить, когда оно появляется из-под воды, чем когда оно погружается в воду.

Для плотин с пологой вершиной опыты хорошо подтверждают теоретическое значение коэффициента а = = О, 577.

Рис. 137. Приспособление для отсчета уровня свободной поверхности воды

См., например, статью Рэбока (Rehbock) в книге De Thierry und Matschoss, Die Wasserkraftlaboratorien Europas, стр. 104. Berlin, 1926.

f) Сооружения, возводимые в открытых руслах, нарушают равномерное течение. Связанные с этим явления очень подробно изучены гидравликами. Если эти явления развиваются на очень коротком участке реки, то в первом приближении можно пренебречь действием трения; тогда мы получим соотношения, уже рассмотренные в п. 16 предыдущей главы. Однако во многих случаях сопротивление вследствие трения играет столь существенную роль, что его необходимо учитывать. Если вертикальным ускорением всюду можно пренебречь (следовательно, если кривизна свободной поверхности всюду мала), то достаточно рассмотреть только среднее продольное ускорение Тогда

уклон свободной поверхности - в каждой точке будет складываться, во-первых, из уклона, обусловленного трением и соответствующего значениям скорости w и глубины воды h во взятой точке, и во-вторых,

из уклона обусловленного продольным ускорением. Если г есть

б ах

уклон дна русла, то очевидно, что

dz dh dx dx

Уравнением неразрывности в простейшем случае, когда русло очень широко, а глубина постоянна по всей ширине русла, будет

wh = const.

После исключения скорости w мы получим для определения h при заданном уклонена i{x) диференциальное уравнение первого порядка. Для г = const его решение будет, конечно, наиболее простым. По своему характеру это решение будет различным в зависимости от того, является ли невозмущенное течение при заданном уклоне спокойным или стремительным (см. §16 гл. П и § 11 гл. III). Не производя вы-числений, укажем лишь на важнейший их результат: при спокойном течении всякого рода возмущения равновесного состояния распространяются, постепенно затухая, и вниз, и вверх по течению, при стремительном же течении только вниз по течению. Если в последнем случае путем какого-либо насильственного вмешательства, например, путем установки поперек русла щита, возмущения течения вынуждаются распространяться вверх по течению, то это происходит всегда в виде прыжка воды, причем течение между прыжком и препятствием приобретает спокойный характер. На рис. 138 и 139 изображены для двух

Эти вычисления можно найти, например, и книге Forchheimer Ph., цитированной на стр. 220.