ния от нее. Это ни в какой мере не противоречит сказанному выше, так как теперь нельзя отодвинуть контрольную поверхность в бесконечность.

Более подробное исследование показывает, что при движении очень удлиненного тела (см. рис. 57) равно нулю не только сопротивление в целом, но также результирующие силы давления и на переднем, и на заднем конце тела.

При ускоренном движении тела в жидкости без трения сопротивление возникает, однако это сопротивление такого рода, как если бы масса тела увеличилась на величину массы жидкости, увлекаемой телом при своем движении. Для шара величина такой присоединенной массы равна половине массы жидкости, вытесняемой шаром. Так как при возникновении движения из состояния покоя вначале образуется всегда приближенно потенциальное течение, то понятие о присоединенной массе имеет значение и для реальных жидкостей.

Равенство нулю сопротивления тела, равномерно движущегося в жидкости без трения, можно вывести также из энергетических соображений. В самом деле, при отсутствии трения работа, необходимая для преодоления сопротивления, может накапливаться в жидкости только в виде кинетической энергии. Между тем при потенциальном течении, когда жидкость позади равномерно движущегося тела так же смыкается, как расступается впереди него, за телом не остается никакого возмущения течения, в котором могла бы накапливаться кинетическая энергия. Следовательно, при таком движении не может быть и сопротивления. Однако могут быть и такие случаи движения в жидкости без трения, когда позади тела в жидкости остается кинетическая энергия и, следовательно, возникает сопротивление. Одним из таких случаев является движение крыла самолета, упомянутое в §13, п. Ь); подробно это движение будет рассмотрено в § 17 и 18 при изложении теории крыла самолета. Возникновение подъемной силы без продолжающегося накопления в жидкости кинетической энергии не противоречит закону сохранения энергии, так как подъемная сила перпендикулярна к пути тела в жидкости и поэтому при установившемся движении для ее сохранения не требуется никакой затраты работы. Вопрос о возникновении подъемной силы был нами уже рассмотрен в §11 предыдущей главы.

Другим примером, когда в жидкости без трения позади движущегося тела остается кинетическая энергия, является движение корабля на свободной поверхности жидкости. Как уже было сказано в § 13, п. Ь), в этом случае позади корабля образуется расширяющаяся система волн, в которой происходит рассеяние энергии. Этому рассеянию энергии соответствует волновое сопротивление.

Возникновение сопротивления при ускоренном движении также легко понять с точки зрения закона сохранения энергии. В самом деле, если бы сопротивление при таком движении не возникало и, следовательно, не требовалось бы силы для преодоления этого сопротивления, то присоединенная масса не могла бы накапливать кинетическую энергию.

В действительности полное сопротивление почти всех тел значительно больше всегда неизбежного сопротивления трения (см. §3 и 5). Причина этого заключается в том, что при движении таких тел образуются поверхности раздела и вихри, описанные в § 6. Именно эти вихри и являются основной причиной сопротивления. Они препятствуют смыканию потока позади обтекаемого тела и обусловливают несимметричное распределение давления на поверхности тела; кроме того, для их образования требуется постоянная затрата энергии.

Ь) Из различных попыток определить сопротивление тел, не выходя из рамок теории идеальной жидкости, рассмотрим две, наиболее типичные, предпринятые Кирхгофом и Карманом.

Кирхгофе исследовал обтекание плоской пластинки, поставленной перпендикулярно к потоку (рис. 141). Перед пластинкой поток разделяется и затем сбегает с ее краев, образуя поверхности раздела. Позади пластинки пространство между поверхностями раздела заполнено покоящейся жидкостью. Так как давление в этом пространстве,если пренебрегать силой тяжести, везде одинаковое, то должно быть одинаковым также давление во всех точках поверхностей раздела, следовательно, на основании теоремы Бернулли, должна быть одинаковой и скорость. Вычисления показывают, что при соблюдении этого условия возможны только такие решения задачи, при которых поверхности раздела простираются до бесконечности, а скорость на поверхностях раздела равна скорости невозмущенного потока, т. е. скорости жидкости в бесконечности. Что касается распределения давления, то перед

пластинкой в ее центре мы имеем динамическое давление ; по мере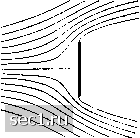

Рис. 141. Обтекание плос кой пластинники с образо ванием поверхностей раз дела

iKirchhoff, Zur Theorie freier Fliissigkeitsstrahlen. Crelles Journ., т. 70 (1869).

приближения к краям пластинки давление уменьшается и на краях делается равным давлению в невозмущенном потоке; на задней стороне пластинки имеет место постоянное давление, равное давлению в невозмущенном потоке. Отсюда следует, что сопротивление пластинки пропорционально ее площади и динамическому давлению, и поэтому коэффициент сопротивления с должен иметь постоянное значение. Согласно вычислениям Кирхгофа, это значение равно

с = = 0,880.

4 -- 7Г

Однако в действительности, как уже неоднократно подчеркивалось, поверхности раздела очень неустойчивы и быстро распадаются, образуя большие и малые вихри. Поэтому зона мертвой воды за пластинкой не доходит до бесконечности, и поток на некотором расстоянии за пластинкой опять смыкается. В связи с этим давление позади пластинки значительно ниже, чем в невозмущенном потоке. Таким образом, задняя поверхность пластинки оказывает подсасывающее действие, и сопротивление получается значительно больше, чем по расчетам Кирхгофа. Для бесконечно широкой пластинки (т.е. практически для пластинки, ограниченной параллельными боковыми стенками) измерения показывают, что с = 2,0. При обтекании прямоугольных пластинок с конечным отношением сторон жидкость огибает узкие стороны и попадая в подсасывающее пространство, значительно уменьшает существующее в нем разрежение. Для различных отношений сторон прямоугольника эксперимент дает следующие значения коэффициента сопротивления:

отношение сторон = 1:20 1:10 1:4 1:1 с= 1,45 1,29 1,19 1,10

Расчет Кирхгофа относится к бесконечно длинной пластинке, следовательно, он очень плохо согласуется с результатом опыта. Наоборот, хорошее совпадение расчета с опытом получается в том случае, когда при обтекании водой пластинки пространство позади пластинки заполняется воздухом (или парами жидкости, как это имеет место при очень высоких скоростях). В этом случае поверхности раздела совсем или почти не распадаются, и поэтому условия, положенные в основу теории, хорошо удовлетворяются. На рис. 142 изображена такая устойчивая поверхность раздела, получившаяся в результате выстрела в воду через стенку стеклянного сосуда.