Рис. 154. Старые Рис. 155. Современные

профили крыльев профили крыльев

В прежние годы при конструировании самолетов обычно стремились получить возможно большую подъемную силу. В настоящее время главными требованиями, предъявляемыми к самолету, являются высокая скорость полета и легкая управляемость. Эти требования привели к разработке новых типов профилей, некоторые из которых изображены на рис. 155. Самый нижний из них имеет особенно малое лобовое сопротивление, следовательно, он особенно пригоден для скоростных самолетов.

Отличительной особенностью профилей, удовлетворяющих требованию легкой управляемости самолета, является неизменное положение центра давления на крыле (см. ниже, стр. 272).

Как уже было упомянуто в предыдущем параграфе, можно сохранить пограничный слой около крыла на значительном протяжении ламинарным и тем самым уменьшить сопротивление трения, если переместить место наибольшей толщины профиля возможно дальше назад - к концу профиля. Самый нижний профиль на рис. 155, а также профиль Ъ на рис. 156 имеют именно такую форму. В верхней части рис. 156 изображено распределение

LilienthalO., Der VogeLflug als Grundlage der Eliegekunst, 1889. Lewis G. W., Journ. of the Roy. Aeron. Soc. 1939 (май),

лом атаки). Однако, как доказал в 1873 г. опытным путем Лилиенталь, значительно лучше в этом отношении немного изогнутые пластинки. Тонкие пластинки с успехом могут быть заменены довольно толстыми пластинками с профилем, напоминающим рыбу (рис. 149). Вполне пригодны даже очень толстые крылья, как это доказал в 1917 г. Юнкере (Н. Junkers), построивший цельнометаллический самолет с крыльями, воспринимавшими нагрузку только при помощи системы внутренних подпорок (лонжеронов и нервюр), скрытых внутри крыла. Некоторые профили крыльев старых типов изображены на рис. 154; они очень похожи на профили крыльев хорошо летающих птиц.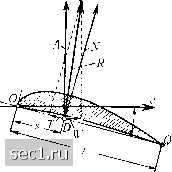

Рис. 156. Теоретическое распределение давления на поверхности двух симметричных профилей при угле атаки в 0°

Рис. 157. Разложение полной силы сопротивления R на подъемную силу А и лобовое сопротивление W, а также на нормальную и касательную силы N и Т

давления, вычисленное Тани и Митуизи" для двух профилей: для профиля а старого типа и для современного скоростного профиля Ь, имеющего только что указанную форму. Оба эти распределения, полученные путем теоретических вычислений, хорошо согласуются с экспериментом. Измерения сопротивления, выполненные при угле атаки в 0° и при числе Рейнольдса R = 3-10®, дали следующие значения коэффициента сопротивления Cw- для профиля (а) Си, = 0,0063, для профиля (Ь) Си, = 0,0030.

Для получения численных характеристик свойств крыла результирующая сила сопротивления R разлагается на две составляющие (рис. 157): либо на уже упомянутые подъемную силу А и лобовое сопротивление W, действующие в направлениях, перпендикулярном и параллельном направлению движения, либо на нормальную силу N и касательную силу Г, действующие в направлениях, перпендикулярном и параллельном какой-нибудь линии профиля, например, его хорде, т. е. прямой, соединяющей переднюю и заднюю точки профиля. Так как площадь проекции крыла на плоскость, перпендикулярную к направлению движения, зависит от угла атаки, то для удобства вычислений принято относить безразмерные коэффициенты указанных выше сил не к этой переменной площади, а к постоянной площади F наибольшей проекции

Tani and Mituisi, Report Aeronaut Research Institute, Toliio Imp. Univ., т. 4 (Zerich, 1942), стр. 179, в которой приводятся результаты швейцарских исследований.

крыла. В случае прямоугольного крыла эта площадь равна F = lb, где I есть размах крыла (размер в направлении, перпендикулярном к движению), а Ь - ширина крыла (размер в направлении движения). По-прежнему обозначая динамическое давление через pd, мы можем написать:

А = CaFpd; W = cFpd,

. N = CnFpa; Т = ctFpa,

где Са, с, Сп Ct суть коэффициснты подъемной силы, лобового сопротивления, нормальной силы и касательной силы. Силы А и W, с одной стороны, и силы N и Т, с другой, представляют собой составляющие одного и того же вектора R по осям двух прямоугольных систем координат, повернутых одна относительно другой на угол а, образуемый хордой крыла с направлением движения; поэтому для перехода от сил А и W к силам N и Т и обратно применимы формулы преобразования координат, известные из аналитической геометрии. Разделив эти формулы на Fpd, мы получим формулы для пересчета коэффициентов и Сц, в коэффициенты с„ и с*, и обратно. Первые формулы имеют вид:

(Сп = Са COS а + с sin а,

\ Ct = -Са sin а + cos а.

Картина течения вокруг крыла зависит от угла атаки а, поэтому коэффициенты Са и Сц,, а следовательно, на основании формул (89), также коэффициенты с„ и ct являются функциями угла атаки а. На рис. 158 показано типичное изменение этих функций для самого верхнего из профилей, изображенных на рис. 155, причем для случая, когда отношение размаха крыла к его ширине равно 5 : 1. В области углов атаки от А до В обтекание крыла происходит плавно, т.е. поток на всем протяжении крыла прилегает к нему (рис. 159). Наоборот, в области углов атаки, лежащих слева от Л и справа от В, обтекание крыла происходит с отрывом потока на нижней или верхней его поверхности (рис. 160). Пространство между оторвавшимся потоком и поверхностью крыла заполняется вихрями, поэтому, как только возникает отрыв, лобовое сопротивление значительно повышается, а подъемная сила, наоборот, значительно понижается.

Кривые, изображающие зависимость коэффициентов с и Сц, от угла атаки (рис. 158), можно объединить в одну кривую следующим образом: значения с и с, соответствующие общему значению угла атаки а, откладываются в прямоугольной системе осей как абсциссы