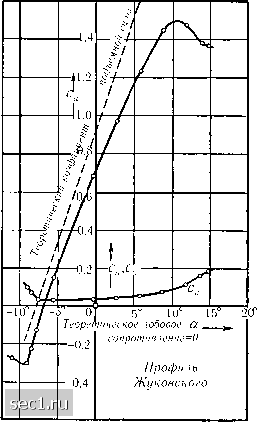Рис. 164. Коэффициенты подъемной силы и лобового сопротивления при плоском обтекании крыла

всегда следует иметь в виду, когда сравниваются результаты теории с результатами опыта.

С точки зрения теории наиболее простым случаем является обтекание крыла бесконечного размаха. Практически условия обтекания такого крыла осуществляются на крыле конечного размаха, вплотную прилегающего своими боковыми концами к двум параллельным стенкам. Установившееся движение жидкости без трения около такого крыла представляет собой потенциальное течение с циркуляцией (см. § 11

Kutta W. М., Sitzungsber. d. Bayr. Akad. d. Wiss., M.-Ph. Kl. 1910 и 1911.

Жуковский Н. е., Z. f. Flugt. u. Motor., т. I (1910), стр. 281; см. также Жуковский Н. е., Aerodynamique, Paris, 1916 [перевод на французский язык книги Н.е.Жуковского, «Теоретические основы воздухоплавания», Москва, 1911 {Прим. перев.)].

Здесь, а также в следующем параграфе, дана соверщенно неверная историческая картина развития теории крыла. Ссылаясь всего только на две работы великого русского ученого Н. е. Жуковского, автор обходит полным молчанием другие работы Н.е.Жуковского, а также С.А.Чаплыгина. Между тем развитие современной теории крыла началось именном с замечательных работ Н.е.Жуковского и С.А.Чаплыгина и было продолжено трудами многочисленных советских ученых. Наиболее важными работами Н.е.Жуковского и С.А.Чаплыгина являются следующие: Ж у к о в с к и й Н . е ., о присоединенных вихрях (1906); Жуковский Н. е., о контурах, поддерживающих поверхности аэроплана (1910) (на эту работу ссылается л. Прандтль); Жуковский Н. е., Геометрическое исследование о течении Кутта (1910); Жуковский Н.е., о поддерживающих планах типа «Антуанетт» (1911) (все эти работы переизданы в «Избранных сочинениях» Н.е.Жуковского, т. II, Москва, 1948), Чаплыгин С. А., о давлении плоскопараллельного потока на преграждающие тела (1910); Чаплыгин С. А., Результаты теоретических исследований о движении аэропланов (1910-1911); Чаплыгин С. А., К общей теории крыла аэроплана (1922); Чаплыгин С. А., о влиянии плоскопараллельного потока воздуха на движущееся в нем цилиндрическое крыло (1926); Чаплыгин С. А., Теория рещетчатого крыла (1911); (в этой работе были предугаданы свойства разрезного крыла, осуществленного только в 1918 г., см. стр. 197); Чаплыгин С. А., Схематическая теория разрезного крыла аэроплана (1921); Чаплыгин С. А. и Голубев В. В., К теории подкрылка и закрылка (1935) (все эти работы переизданы в «Собрании сочинений» С.А.Чаплыгина, т. II, Москва, 1948). См. также следующие работы: Голубев В. В., Исследования по

гл. II). Насколько хорошо эта теория, развитая Кутта и Жуковским, согласуется с опытом, показывает рис. 164. На этом рисунке даны для профиля Жуковского (нижний из профилей, изображенных на рис. 154) теоретические и экспериментальные значения коэффициентов подъемной силы и лобового сопротивления. Теоретическое лобовое сопротивление равно нулю, действительное лобовое сопротивление в основном состоит из сопротивления трения. Действительная подъемная сила несколько меньше теоретической, что также объясняется трением, влияние которого равносильно небольшому уменьшению угла атаки (пограничный слой на верхней стороне крыла по мере приближения к его задней кромке утолщается; это уменьшает циркуляцию, что равносильно уменьшению угла атаки). В области углов атаки, соответствующих безотрывному обтеканию, теоретическое распределение давления вдоль профиля Жуковского хорошо совпадает с практически измеренным распределением давления, если только учесть упомянутое уменьшение угла атаки.

теории разрезного крыла (Труды ЦАГИ, вып. 147, 1933); Голубев В. В., О влиянии надстроек на подъемную силу крыла (Труды ЦАГИ, вып. 342, 1938); Голубев В. В., Теория крыла аэроплана в плоскопараллельном потоке, изд. второе, Москва, 1938. О советских работах по теории крыла при полете при близзвуковых и сверхзвуковых скоростях см. сноску на стр. 394 и 405. (Прим. перев.)

iKarman und Trefftz, Zeitschr. f. Flugt und Motorl. т. 9 (1918), стр. 111.

Mises R., Zeitschr. f. Flugt und Motorl. т. 8 (1917), стр. 157; т. II (1920), стр. 68 и 87.

Более старые из них перечислены в книге Fuchs, Hopf und Seewald, Aerodynamik, т. 2, изд. 2-е, стр. 67-82.

"Theodorsen Th., NACA-Report № 411 (1931); Theodorsen Th. and Garrick J. E., NACA-Report № 452 (1933).

Betz A ., Luftfahrtforschung, т. 11 (1934), №6; далее Mangier W., Jahrb. f. D. Luftfahrtforschung, т. I (1938), стр. 46.

eGarrick.I.E., NACA-Report № 542 (1936).

Кутта и Жуковский изучили профили, получавшиеся следующим образом: окружность, обтекаемая жидкостью в плоскости , конформно отображалась на плоскость z таким образом, что другая окружность, пересекавшая в плоскости первую (или касавшаяся ее), переходила в прямолинейный отрезок на плоскости z. Однако таким путем удавалось получить профили только вполне определенного вида. Карман и Треффц, используя конформное отображение кругового двуугольника, получили ряд других профилей. Ми-зес указал отображения, которые дают многие другие профили, в том числе и профили с постоянным центром давления. В результате многочисленных дальнейших работ, из которых особо следует упомянуть работы Теодореса и Гаррика**, были разработаны методы, позволяющие рассчитать потенциальное течение с циркуляцией около любого заданного профиля, следовательно, позволяющие вычислить также распределение давления вдоль профиля. Был найден способ приближенного решения и обратной задачи: отыскания профиля, на котором имеет место заданное распределение давления®. Далее были разработаны теоретические методы для расчета двухмерного обтекания биплана. В этой области фундаментальное значение имеет работа Гаррика®; полученные им результаты применимы также к разрезному крылу и к крылу с подвесным закрылком.

Наряду с перечисленными способами расчета обтекания крыла, основанными на применении конформного отображения, разработан приближенный способ, основанный на замене крыла системой вихрей, расположенных в горизонтальной плоскости (вообще говоря, крыло следует заменять системой вихрей, расположенных на поверхности, проходящей через скелетные линии профилей, образующих крыло, но это вносит очень большие математические трудности). Этот способ, который может быть применен также к трехмерным задачам, для двухмерных задач дает особенно простые соотношения. Так, например, для зависимостей коэффициентов подъемной силы и момен-