только в том случае, если распределение подъемной силы вдоль размаха изображается половиной эллипса (рис. 168). Так как при таком распределении подъемной силы циркуляция в середине крыла в раз больше своего среднего значения и, кроме того, отдельные вихревые нити в среднем лежат ближе к середине крыла, чем в случае упрощенной системы вихрей, то скорость w должна быть больше полученного выше значения Wq. Выполнение интегрирования для всех вихревых нитей дает для скорости W значение:

Рис. 168. Эллиптическое распределение подъемной силы

W = 2w(i =

2А KpvP

(92)

Эта скорость, складываясь со скоростью v набегающего потока, приводит к отклонению его от первоначального направления на угол if, определяемый из соотношения

TTpV

(93)

Так как скорость w при эллиптическом распределении подъемной силы остается, как было сказано, постоянной по всему размаху, то остается постоянным и угол if. Поэтому в данном случае непосредственно применимо соотношение (91), которое теперь принимает вид:

Wi =

(94)

Это сопротивление, возникающее при движении крыла конечного размаха в жидкости без трения, называется индуктивным сопротивлением (такое название дано ввиду формальной аналогии рассматриваемого явления с электромагнитной индукцией). Скорость w, вызванная крылом, называется индуктивной скоростью. Более подробное исследование показывает, что индуктивное сопротивление, определяемое формулой (94) в виде функции от подъемной силы А, является минимальным при заданном размахе /. При всех других распределениях подъемной силы.

Подчеркнем еще раз, что здесь имеется в виду минимум для заданного размаха. Увеличение размаха при сохранении распределения подъемной силы ведет к даль-нейщему уменьщению индуктивного сопротивления. Конечно, на практике размах крыла не может быть сделан особенно большим (главным образом вследствие ограниченной прочности материалов).

Подробные сведения об индуктивном сопротивлении для простых (моноплан-ных) и сложных (бипланных) крыльев можно найти в книге: Юрьев Б . Н ., Экспериментальная аэродинамика, ч. 2, Москва 1938; см. также книгу: Голубев В. В., Теория крыла аэроплана конечного размаха. Труды ЦАГИ, вып. 108, Москва 1931. [Прим. перев.)

отличающихся от эллиптического, индуктивное сопротивление получается больше.

Минимальное свойство формулы (94) связано с постоянством индуктивной скорости вдоль размаха. Так как функция вблизи своего минимума изменяется обычно незначительно, то формулу (94) можно применять как приближенную формулу также для других распределений подъемной силы, при условии, что они не очень отличаются от эллиптического распределения. В частности, это вполне допустимо для прямоугольного крыла с не очень малым относительным размахом.

Формула (94) показывает, что индуктивное сопротивление, связанное с возникновением подъемной силы, тем меньше, чем на большем размахе распределена подъемная сила. Именно по этой причине крылья всех самолетов имеют размах, значительно больший, чем ширина крыла. Последняя не входит в формулу (94), что означает следующее: величина индуктивного сопротивления зависит от состояния потока позади крыла, но не от того, как это состояние создается: на малой ли ширине большими разностями давлений или на несколько большей ширине малыми разностями давлений.

Исследование возмущения, остающегося позади крыла при его движении, приводит к другому, весьма наглядному выводу формулы (94). Быстро движущееся крыло, встречая на своем пути s все новые и новые массы воздуха, в течение очень короткого времени давит последовательно на каждую из этих масс. Вместо этого можно представить себе, что крыло давит мгновенно на массу воздуха на протяжении s всего своего пути подобно доске, имеющей размах / и ширину s и получающей резкое ускорение вниз. При таком мгновенном давлении возникает плоское потенциальное течение (см. §10 п. с) гл. II), причем поверхность, на которую действует давление, превращается в поверхность раздела. Картина такого течения изображена на рис. 169. Ударные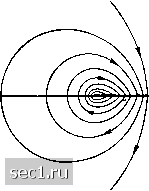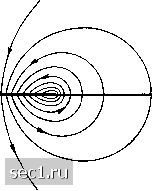

Рис. 169. Течение позади крыла

давления

pdt,

определяющие это течение, можно связать, с одной стороны, с потенциалом скоростей, а с другой стороны - с распределением подъемной силы. Выполняя вычисления, мы придем опять к соотношению (94).

Вычисления производятся следующим образом. Если пренебречь квадратами скоростей, вызванных возмущением течения, то уравнение (39) гл. II примет вид:

дФ , Р Роо

+ -=const=-,

где Рас есть невозмущенное давление в бесконечности. Интегрируя по времени от начала удара до его конца и принимая, что до удара везде было Ф = О, мы получим:

fip-

Poo)dt = 0.

Обозначим давление под поверхностью раздела во время удара через рн, а над поверхностью раздела - через рв; тогда мы будем иметь:

(р„-рв)Л = р(Фв-Ф„) = /9г.