с.2 = с1+г(-). (106)

Для прямоугольного крыла F = lb, следовательно, отношение равно р т. е обратной величине относительного размаха / : Ь. Хотя формула (106) для пересчета коэффициента лобового сопротивления выведена в предположении, что подъемная сила крыла исчезающе мала, однако она дает для крыльев с относительным размахом от 3:1 до 7:1 очень

угол атаки, а интенсивность подъемной силы, определяемую, например, коэффициентом подъемной силы Са- (Правда, этот коэффициент представляет собой не что иное, как среднее значение интенсивности подъемной силы, изменяющейся от середины крыла к его концам; однако использование этого среднего значения не должно внушать никаких опасений, так как в области безотрывного обтекания коэффициент Са связан с углом атаки а приблизительно линейной зависимостью, а коэффициент профильного сопротивления Су,р изменяется не очень сильно.) Из формулы (94) мы имеем:

с .-

Ого! - ,2 • ТГГ

Подставляя ЭТО ЗН8ЧвНИв Cyji в равенство (104), мы получим:

Cw = Cwp + Cwi = Cwp + (105)

Это соотношение может быть использовано для определения коэффициента лобового сопротивления крыла конечного размаха, если известен из опыта коэффициент лобового сопротивления бесконечнодлинного

крыла или другого конечного крыла с другим отношением -. В послед-

нем случае получается более точный результат, так как распределение подъемной силы вдоль размаха для обоих крыльев приблизительно одинаковое, и упомянутое выше составление среднего значения коэффициента подъемной силы производится для обоих крыльев. Применяя соотношение (105) один раз к крылу 1 (размах /i, площадь Fi), а другой раз - к крылу 2 (размах /2, площадь 2) и имея в виду, что, согласно сказанному выше, Са2 = Cai, мы получим:

120 100 80 60 40 20 О

--20

100с,

*- 2 «-3 --4 -5

100с,

Рис. 170. Поляры для семи прямоуголь- Рис. 171. Пересчет эксперимен-ных крыльев с различными относитель- тальных результатов, изображенными размахами. Числа для Са и Сц, уве- ных на рис. 170, к относительному личены в 100 раз размаху 5:1. Числа для Са и

увеличены в 100 раз

хорошие результаты при всех значениях подъемной силы. При безотрывном обтекании таких крыльев линии тока отклоняются от своей невозмущенной (т. е. прямолинейной) формы, если не считать непосредственной близости к крылу, очень незначительно. Крылья с относительным размахом 2:1 или тем более 1:1 заменять несущим вихрем можно только с очень большой натяжкой, и поэтому для них нельзя требовать, чтобы результаты опыта совпадали с теоретическим подсчетом; тем не менее, и в этих случаях формула (106) дает довольно хорошие результаты. О степени точности формулы (106) дают представление результаты экспериментов, изображенные на рис. 170 и 171. На рис. 170 построены на основании данных опыта поляры для семи прямоугольных крыльев с одним и тем же профилем, но с разными относительными размахами (от 1:1 до 7:1). На рис. 171 все экспериментальные значения коэффициента Су, пересчитаны по формуле (106) к относительному размаху 5:1. Мы видим, что преобладающая часть точек после пересчета располага-

ется очень тесно около поляры, полученной в результате эксперимента для относительного размаха 5:1. Наибольшее несовпадение с этой полярой дают точки, соответствующие квадратному крылу.

Индуктивному сопротивлению в системе координат Са, Су, соответствует парабола, называемая параболой индуктивного сопротивления. Если провести такую параболу на одном чертеже с полярой, полученной из опыта (рис. 172), то отрезки прямых, соединяющих точки обеих кривых параллельно оси Су,, будут, на основании уравнения (105), численно равны значениям коэффициента профильного сопротивления.

Аналогичным образом производится пересчет углов атаки при переходе от одного относительного размаха к другому. Углу атаки а бесконечно длинного крыла в горизонтальном потоке соответствует угол атаки а крыла конечного крыла (см. рис. 165). Угол а меньше угла а на величину if, так как конечное крыло вызывает скос потока

на угол if, зависящий от относительного размаха. Поэтому можно предполагать, что зависимости между коэффициентом подъемной силы Са и истинным углом атаки а = а - ip должна быть одинаковой при всех значениях относителного размаха. Согласно равенству (93) мы имеем: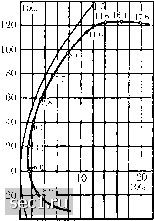

Рис. 172. Парабола индуктивного сопротивления

tgip =

следовательно, вводя обозначение

а = fiCa),

и имея в виду, что можно принять tg ip м ip, мы можем написать:

a = a + = fica) + -.

(107)

Применяя это уравнение один раз к крылу 1 с размахом li и площадью Fl, а другой раз к крылу 2 с размахом /г и площадью F2, мы