трона также квантовано, т. е. угол между плоскостью орбиты и направлением напряженности поля принимает дискретные значения. При этом квантуется проекция магнитного момента на направление внешнего поля:

\>Ш="1\>-в, (111)

где т-- магнитное квантовое число, которое может принимать как положительные, так и отрицательные целочисленные значения, включая нуль.

,Из (1.4) и (1.11) следует, что а-arccos т/п, но, как увидим далее, расчеты по этой формуле расходятся с данными опыта. Это доказывает несовершенство модели Бора.

Экспериментальные данные, не объясняемые моделью Бора. Теория Бора была крупным достижением в области изучения атома. Однако и она не объясняла многие экспериментальные данные. Рассмотрим некоторые из них.

Магнитомеханические (гиромагнитные) опыты Эйнштейна и де Гааза, впервые осуществленные в 1915 г., показали связь между механическим и магнитным моментами атома "Jlhfi (рис. 1.1). На тонкой упругой нити / помещался образец 2 в виде цилиндра диаметром примерно 0,03 см и длиной 10.см из ферромагнетика (железа) или парамагнитных солей. Образец мог намагничиваться вдоль продольной оси магнитным полем соленоида <?. Поворот стержня можно было фиксировать с помощью оптической системы, состоящей из зеркальца 4, осветителя 5 и шкалы 6.

Под действием магнитного поля магнитные моменты атомов устанавливаются по полю. При изменении направления поля на обратное (коммутировании тока в обмотке катушки) магнитные моменты должны повернуться на 180°, а так как электроны вращаются быстро и их момент количества движения не равен нулю, то должен соответственно измениться полный момент количества движения системы, что невозможно. Поэтому согласно закону сохранения момента количества движения образец повернется на некоторый угол. Для усиления эффекта был использован резонанс между частотой изменения поля и собственной частотой колебаний стержня.

Из опыта можно было непосредственно определить гиромагнитное отношение, которое {в единицах el{2m)] оказалось близким к 2, что противоречит полученному ранее [см. формулу (1.2)] выводу, где отношение орбитального магнитного момента к механическому равно 1. Это несоответствие назвали гиромагнитной аномалией.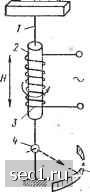

Рис. 1.1. Схема опыта Эйнштейна и де Гааза

сеченое •цслюсвв тгнита.

Данные, полученные Эйнштейном и де Гаазом, совпадали с расчетными, основанными на эффекте Барнетта, открытом" в 1909 г. Барнетт приводил в быстрое движение железный стержень, который намагничивался вдоль продольной оси, что объясняется ориентировкой магнитных моментов вследствие гироскопических свойств электрона.

Опыт Штерна и Герлаха был произведен в 1922 г. * Схема опыта показана на рис. 1.2. Из печки 1 выходит поток испарившихся молекул или атомов, на который действует магнитное поле электромагнита 2; диафрагмы 3 служат для создания узкого пучка; экран 4 представляет собой пластинку, на которой можно обнаружить следы осевших частиц. Поле электромагнита в одном из, направлений (на рис. 1.2 по оси z) должно быть неоднородным, что достигается специальной формой полюсных наконечников. В этом случае на атом, обладающий магнитным моментом р, направленным под углом 6 к направлению градиента поля по оси Z, действует сила

/r [,££ cose, (1.12)

dz

которая существует на участке длиной а. Движение на этом участке равномерно ускоренное. Поэтому отклонение (по оси z) в конце участка

/ dB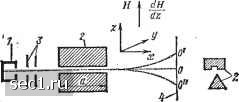

Рис. 1.2. Схема опыта Штерна и Герлаха

Zb--

2 cos е.

(1.13)

где т - масса атома; t-время пролёта через поле на участке а.

В качестве испаряемого вещества Штерн и Герлах использовали серебро. В дальнейшем опыты были проделаны со щелочными металлами и атомарным водородом.

На рис. 1.3 .приведена фотомикрограмма «осадка» для атомов и молекул натрия.

При низких температурах большинство атомов образует молекулы Na2, у которых результирующий магнитный момент равен нулю и отклонение отсутствует.

Атомарное состояние характеризуется двугорбой кривой, т. е. На пластинке образуются две полоски, расположенные симметрич-

* Несколько ранее аналогичный опыт был произведен П. Л. Капицей и Н. Н. Семеновым.

** Магнитная индукция В=уН, тп& Цо - магнитная постоянная; Н - напряженность магнитного поля.

«(7 I I

HO относительно среднего положения. Дублеты получаются не только для Na, но и для всех других атомов, имеющих один валентный электрон.

Это свидетельствует о пространственном квантовании магнитного момента. Действительно, если бы все значения были равновероятны, на пластинке образовалась бы сплошная полоса между точками О и О" (см. рис. 1.2); одна из этих точек соответствует значению 6 = 0 (расположению магнитного момента параллельно

полю), а вторая - значению 6= =180° (антипараллельному рас-.Nal ММ Na, положению магнитного момента

и поля).

Опыт Штерна и Герлаха позволил рассчитать [по формуле (1.13)] проекцию магнитного момента атома на направление внешнего поля, которая оказалась равной магнетону Бора.

Модель Бора не объясняет результаты рассмотренного опыта. Известно, что атомы водорода, серебра, щелочных металлов и других элементов первой группы не обладают орбитальными механическими и магнитными моментами (далее рассмотрено подробнее). Следовательно, для таких атомов вообще не должно наблюдаться отклонение.в магнитном поле. Кроме того, по правилу пространственного квантования, если бы даже п-\, магнитное квантовое число т в соответствии с возможными, по Бору, значениями для cos а при /2=1 должно было равняться -Ы,0, -1, т. е. на пластинке должны были образоваться три полоски вместо наблюдаемых двух. Модель Бора не объясняет также аномальный эффект Зеемана, тонкую структуру спектральных линий и многое другое.

Квантовая модель. Основной недостаток теории Бора заключается в том, что она представляла собой компромиссное сочетание классической физики с квантовой теорией излучения. Методологически теория Бора требовала решения задач средствами классической физики с последующим отбором дискретных величин, удовлетворяющих требованиям квантовой механики. Выводы теории Бора оказались справедливыми лишь для самых простейших случаев.

Последовательное применение квантовой теории внесло поправки в некоторые из приведенных ранее формул квантования:

квантование орбитального момента количества движения [ср. с формулой (1.3)]

Рис.

10 30 50 70 SO ~ Рошат/я микрометра -

1.3. Фотомикрограмма «осадка» для атомов и молекул натрия

(1.14)