возникновения самопроизвольной намагниченности, т. е. установить критерий ферромагнетизма.

Общее решение этой задачи, приведенное, например, в [1.8], весьма сложно и требует громоздких математических выкладок. В настоящей книге приводится лишь общий ход решения задачи и конечные результаты.

Для установления некоторых важных исуодных понятий рассмотрим вначале одну из простейших атомных структур - молекулу водорода.

На рис. 1.15 схематически показано расположение электронов и ядер молекулы водорода, состоящей из двух атомов. Определим энергию системы в зависимости от расстояния R между ядрами а и Ь. Для это- Рис 1.15. Схематическое изобра-го обратимся к основному уравне- ение расположения электронов и нию нерелятивистской квантовой ме- Р молекуле водорода ханики - волновому уравнению

Шредингера, которое можно представить в следующем виде:

Дф+-[-(-. У. «=0, (1.115)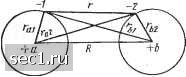

где Д =

Q 2 д 2 Q 2 оператор Лапласа; ф=ф (л:, J/, z)-волновая функция, зависящая от координат х, у, z микрочастицы*; т, Е, и - масса, полная энергия и потенциальная-энергия частицы соответственно.

Важнейшими положениями квантовой механики являются:

1) корпускулярно-волновой дуализм, заключающийся в том, что микрочастицы обладают одновременно как свойствами корпускул, так и волновыми свойствами;

2) вероятностный характер описания поведения отдельных частиц.

Волновая функция не имеет непосредственного физического смысла и не может рассматриваться как волна в пространстве. С помощью волновой функции можно лишь Предсказать вероятность того, что в определенный момент времени частица будет находиться в соответствующей точке пространства. В общем случае функция может быть комплексной; квадрат модуля этой функции, т. е. пропорционален плотности вероятности нахождения частицы в точке с координатами х, у, z.

Уравнение Шредингера для системы, содержащей два электрона и два ядра (рис. 1.15), можно представить следующим образом:

-далее.

Волновая функция зависит также от спиновой переменной с, что учтено

А1 + Д2+(-)

ф=0. (1.116)

Здесь

=(.Xi, У1, Zi; Х2, У2, Zz), (1-117)

где Х\, у\, Z\\ Xi, у2, Z2 - пространственные координаты первого и второго электронов;

и - потенциальная энергия системы, равная сумме взаимодейст-

, , е2 е2 вин: между протонами (ядрами) -- , электронами-,

между электронами и протонами--,--,

е2 е2]

поэтому .

=-i(-i-+-L !------[---(1.119)

Решение уравнения (1.116) обычно проводят методом последовательных приближений.

В нулевом приближении рассматривают систему, состоящую и» двух изолированных атомов {R-oo) с электронами, находящимися в s-состояниях. Полная энергия такой системы Е=2Ео, где Ео - энергия каждого из невзаимодействующих атомов.

Обозначим через 1а{1) волновую функцию электрона 1 в поле ядра атома а, через ь{2) -волновую функцию электрона 2 в поле ядра атома Ь. Тогда волновую функцию двух электронов можна представить в виде ij)(i, 2)=\а{1)1ь{2). Такое представление основано на вероятностном характере волновых функций и на том, что (вероятность осуществления двух независимых событий равняется произведению вероятностей осуществления каждого из событий.

Дальнейшие рассуждения базируются на квантовомеханиче-ском принципе тождественности частиц, который можно сформулировать следующим образом: все физические свойства различных экземпляров электронов аналогичны друг другу. Поэтому, если один из электронов заменить другим, то в рассматриваемой ситуации ничего не изменится.

Для нашего случая это выглядит так: если электрон 2 помес:, тить в состояние а, занимаемое электроном 1, а электрон 1 поместить в состояние Ь, занимаемое электроном 2, т. е. поменять электроны местами, то ничего не изменится. Следовательно, волновая

функция {2, l)=\pa(2)ib(l), получившаяся в результате такого обмена, также является решением уравнения Шредингера.

Таким образом, одной и той же энергии системы 2Ео соответствуют две различные волновые функции 2) и {2, 1). По терминологии квантовой механики говорят, что система вырождена. Причиной вырождения в данном случае является возможность обмена электронами двух атомов («обменное вырождение»).

Согласно принципу суперпозиции *, общее решение задачи можно представить в виде

фо=-аф„(/)Ч*(2)+Рф„(2)ф,(/). (1.120)

Волновая функция фо описывает состояние системы, в которой 1а2 дает вероятность нахождения электрона / у атома а, а электрона 2 - у атома Ъ; р2 дает вероятность обратного распределения.

После решения задачи в нулевом приближении {R-oo) перейдем к первому приближению - рассмотрению системы при сближении ядер с учетом электростатического взаимодействия между атомами. Влияние спина не учитываем.

Полная энергия системы

E=2Eq±E (1.121)

где Е - поправка, которую получают при учете электростатического взаимодействия атомов.

Предполагают, что волновая функция (1.120) является решением и в случае первого приближения. Задача сводится к подбору значений а, р и удовлетворяющих уравнению Шредингера для всей молекулы водорода.

Анализ показывает (см., нащзимер, [1.81]), что существует два возможных решения:

Ф = а [ФЛ/) % (О Ф« (2)1. (1.122).

которому соответствует энергия

fO)=2fo-fC--, (1.122)

ф1?>а1ф„(/)Ф*(2)-фЛ/)ФЛ2)1, ;" (1.123)

которому соответствует энергия

<2)=2о-{-С-Л. (1.123)

*При1щип суперпозиции заключается в следующем: если квантовая система может находиться в состояниях ipi и ips, то она может находиться и в состоянии, описывамом волновой функцией ipaipi-l-pips, где а и р - произвольные, в общем случае комплексные числа.