центрированную решетку; от 900 до 1401°С (у-фаза)-гранецент-рированную и свыше 1401°С (б-фаза)-опять объемноцентриро-ванную. Кобальт при температуре до 480°С (а-фаза) имеет гексагональную решетку, а в интервале от 480 до 1490°С - кубическую гранецентрированную. Никель независимо от температуры образует гранецентрированную решетку.

На рис. 1.20 представлены кривые намагничивания в разных направлениях монокристаллов железа и никеля. Кривые показывают, что кристаллы являются магнитоанизотропными и направлениями самого легкого намагничивания для монокристалла железа являются ребра ,куба, а для монокристалла никеля - пространственные диагонали; самому трудному намагничиванию для железа соответствуют пространственные диагонали, для никеля - ребра куба. При отсутствии внешнего поля всегда имеет место намагничивание в легком направлении.

Энергия, которая требуется для намагничивания единицы объема вещества, определяется площадью между кривой намагничивания и осью ординат: • ,

E=\vdl. .(1.131)

Поэтому заштрихованные на рис. 1.20 площади представляют собой энергию, которую надо затратить для изменения направления намагничивания от легкого до трудного. Эту энергию называют энергией естественной кристаллографической магнитной анизотропии. Для кубического кристалла ее можно представить следующим образом:

Ek=K-\-Ki (а?а+а1а1+аа?) + /Г2а?аа1, (1.132)

где Ко, Кь К.2 - константы кристаллографической магнитной анизотропии, определяемые экспериментально; «1, «2, ссз - направляющие косинусы вектора намагниченности по отношению к осям х, у, г, совпадающим с основными кристаллографическими направлениями кубической решетки.

Формула (1.132) впервые была получена Н. С. Акуловым, осуществившим значительные исследования в области магнитной анизотропии ферромагнитных кристаллов. Им было установлено, что физической причиной существования анизотропии является магнитное взаимодействие между электронами. В дальнейшем эта идея получила квантовомеханическое обоснование.

До сих пор предполагалось, что кристалл свободен от упругих деформаций. При наличии механических напряжений кроме кристаллографической анизотропии возникает магнитоупругая анизотропия, вызванная дополнительным магнитным взаимодействием атомов в результате искажения реШеткй при деформации. Механические напряжения могут возникнуть в результате изменения магнитного состояния вещества (магнитострикция), а также под действием внешних сил, приложенных к образцу.

Энергия магнитострикционной деформации Е. М а г н и т о-

стрикц.ия - это изменение формы и размеров тела при изменении его магнитного состояния, которое возникает в результате перехода ферромагнитного вещества через точку Кюри при отсутствии внешнего поля (самопроизвольная магнитострикция) и при воздействии внешнего поля на ферромагнетик, температура которого ниже точки Кюри.

Для объяснения явления самопроизвольной магнитострикции рассмотрим переход через точку Кюри модели ферромагнетика в виде шара таких размеров, что в нем образуется только один домен. При переходе вещества от парамагнитного к ферромагнитно-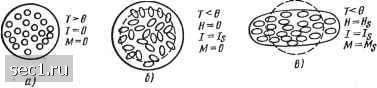

Рис. 1.21. Схема магнитострикции ферромагнетика

му состоянию происходит изменение значения обменной энергии и, как результат этого, скачкообразное изменение магнитного состояния. Обменная энергия по своей природе является изотропной, поэтому изменение вызывает деформацию шара, одинаковую во всех направлениях, т. е. изменение его радиуса. Изменение магнитного состояния связано с магнитными силами в кристаллической решетке, которые, как отмечалось, являются анизотропными, вследствие чего они вызывают различную деформацию в разных направлениях и шар превращается в эллипсоид.

Рассматривая самопроизвольную магнитострикцию модели ферромагнетика в виде шара с многодоменной структурой, нетрудно Заметить, что при переходе через точку Кюри у него изменится радиус и, следовательно, объем, но не изменится форма. Объясняется это тем, что все направления являются равновероятными. Поэтому самопроизвольную магнитострикцию можно рассматривать как объемную.

Магнитострикция, возникающая под действием намагничивающего поля при температуре ниже точки Кюри, объясняется тем, что под действием этого поля появляется результирующий магнитный момент; следовательно, меняется магнитное взаимодействие и Деформируется кристаллическая решетка. При этом мало меняется объем намагничиваемого образца, но сильно меняются его Линейные размеры. Поэтому магнитострикцию под действием внешнего поля можно рассматривать как линейную.

Явление магнитострикции иллюстрируется рис. 1.21, на котором схематически изображены модели ферромагнетика с многодоменной структурой. Рис. 1.21, й представляет собой образец при

температуре выше точки Кюри. Кружками изображены области которые после перехода через точку Кюри образуют домены. На рис. 1.21,6 показан образец после охлаждения ниже точки Кюрв (в виде эллипсов изображены домены); в результате спонтанной магнитострикции радиус шара увеличился, форма не изменилась. На рис. 1.21, в дан образец при температуре ниже точки Кюри, находящийся под действием внешнего поля (образец намагничен до--насыщения); в результате магнитострикции форма образца изменилась, а объем остался прежним.

Н. С. Акуловым было получено следующее выражение для константы магнитострикции is={Al/l)s намагниченного до насыщения кристалла кубической симметрии:

+ ЗХ„1(а,а2р,р2+«2аз№+аза1рзр1). (1.133)

где Яюо и Ящ - константы магнитострикции при намагничивании кристалла до насыщения в направлениях осей [100] и [Ш]; «ь «2, «3 - направляющие косинусы вектора самопроизвольной намагниченности по отношению к кристаллографическим осям; Pi, (Зг, Рз - направляющие косинусы направления, в котором измеряется изменение длины.

Энергия магнитоупругой деформации единицы объема, возникающая вследствие магнитострикции:

Е1=ЕюЖ (1.134)

где Ею - модуль Юнга, который считаем изотропным.

Сумму энергий кристаллографической магнитной анизотропии и магнитоупругой в результате магнитострикции называют общей энергией магнитной анизотропии:

Е,Е,-\-Е,. (1.135)

Магнитоупругая энергия Е. Если материал подвергнуть действию внешних напряжений (однородному растяжению или сжатию), то возникающая при этом магнитоупругая энергия

---о [>ioo(aiY?+a2Y2 + alY3) + 2>.iii (aia2YiY2+

--a2a3Y2Y3 4-aia3YiY3)], ,(1.136)

где Yi, Y2. Y3 - направляющие косинусы оси, вдоль которой действует внешняя сила.

В случае изотропной магнитострикции (слабой анизотропии магнитострикции) Xioof!kni=Ks, и формулу (1.136) можно представить в виде

Е,= --j\ccosv, .(1.137)

где cos ф=а1у1 + a2Y2+ci:3Y3-