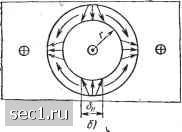ли к исследуемой поверхности, другая половина - отрицательном, чему на рисунке соответствуют светлые и темные участки. При воздействии на пластинку магнитным полем Явн, направленным перпендикулярно ее поверхности, темные лабиринтные домены с антипараллельной приложенному полю ориентацией начинают сжиматься (светлые с параллельной ориентацией - расширяться),

приобретая гантелеобразную форму (рис. 1.33, б). По мере увеличения поля гантелеобраз-ные домены разрываются, и на

их основе при Явн=Ятт возни-

кают домены в форме небольших цилиндров, пронизывающие пластину по толщине сверху донизу (рис. 1.33, в). С ростом поля радиус ЦМД практически линейно уменьшается (рис. 1.33, г) и при некотором значении поля Нва=Нк ЦМД исчезают. Пластина оказывается однородно намагниченной (монодоменное состояние). Отсюда следует, что ЦМД существуют в определенном диапазоне значений поля Явн-

Для качественного объяснения причин образования ЦМД можно провести формальную аналогию между каплей жидкости, находящейся на твердой подложке, и доменом. На каплю действуют два рода сил: сила тяжести, под действием которой капля растекается по поверхности, и силы поверхностного натяжения, старающиеся придать капле форму сферы. На домен в отсутствие поля Явн действуют также два рода сил: силы магнитостатического происхождения, стремящиеся растянуть домен, и силы, связанные с наличием энергии доменной стенки, стремящиеся сжать домен. Количественно в отсутствие внешнего поля это приводит к «растеканию» домена по поверхности с образованием лабиринтной структуры. Если создать Явн, то возникнет сила, связанная с взаимодействием домена с внешним полем, которая стремится сжать домен.

Устойчивость ЦМД в статических полях. Теория устойчивого состояния однородно намагниченного изолированного ЦМД радиуса г, находящегося в бесконечной монокристаллической одноосной пластине толщиной h (рис. 1.34, а), подробно разработана Э. Бобе-ком и Э. Тиле [4.1]. Под устойчивостью понимают способность домена сохранять цилиндрическую форму, характеризуемую Гщах и Гтт, в некотором Диапазоне внешних полей Явн=Ятт-Ятах (поля устойчивого состояния ЦМД). Естественно, что область устойчиво-

Рис. 1.34. Модель изолированного домена в одноосной пластине: я -1 ЦМД во внешнем магнитном поле Н„; S - упрощенная модель располокения вектора намагниченности 1 в центре доменной стенки

сти соответствует минимальному значению полной энергии ЦМД:

Е=Е-Е,-Е. (1.166)

Для нахождения условия минимума полной энергии возьмем производную от £ то г и приравняем ее нулю. Магнитная энергия с учетом изменения знака намагниченности на доменной стенке ЦМД

E=2v.jy=2,HJr4. (1.167)

Сила сжатия при этом Fu=dEMldr=i\x.oHEtJsnrh. Энергия граничной стенки При условии ее бесконечно малой толщины (бгр<С)

E-,=2nrhy,. (1.168)

Сила сжатия за счет стенки Ру=дЕу1дг=2пкутр.

Магнитостатическая энергия ЦМД, находящегося в пластине конечной толщины, намагниченной перпендикулярно поверхности:

Е = - !Хо2Я1/ (N„ -N,), (1.169)

где -Vn, Лд - усредненные по объему домена V размагничивающие факторы по ОЛН для пластины и домена.

В [1.13] приведено упрощенное выражение для Е, позволяющее получить удобную для последующего анализа формулу возникающей силы растяжения в виде

где коэффициент е определяется геометрическими соотношениями в ЦМД-пластине. При 2г г=0-10 8=0,75.

Условие равновесия ЦМД после упрощений примет вид

BH+-i;g- ,+:.2riH =0 (1-171)

или, введя обозначения

Ht= ; Яо=---, (1.172)

получим

Я,„-[-Ят=Яо. (1.173)

Из (1.172) следует, что Ну изменяется сильнее, чем Н, при изменении радиуса домена. Графическое решение уравнения (1.171) приведено на рис. 1.35.

При выбранном поле Нлн=Нвн1 корнями являются точки J и 2. Обе. точки соответствуют экстремальным значениям энергии Е, но минимуму энергии, т. е. устойчивому состоянию, соответствует точка 2, поскольку любое случайное воздействие, уменьшающее радиус домена /"2, вызывает появление силы расширения >£bh+/v, стремящейся вернуть домен в исходное состояние с г=г2.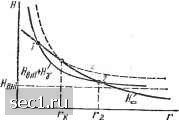

Рис. 1.35. Схематическое изображение зависимостей Я.,, Н , Явн от радизса домена г

Из рис. 1.35 видно, что если Явн=0, то точка 2 находится в области r-voo, т. е. ЦМД не образуются, а имеет место лабиринтная магнитная структура. При небольших полях смещения ЦМД сосуществуют с короткими полосовыми доменами. Эта область носит название области эллиптической неустойчивости. Для изолированного домена переход от лабиринтной структуры к ЦМД и обратно происходит резко в поле Ящт; с ростом напряженности точка 2 переходит в область конечных значений г, что соответствует образованию устойчивых ЦМД, радиус которых с изменением

поля от Ящт до Ящах измсняется от Гтах до Гтт. При дальнейшем увеличении Явн точки 1 и 2 сближаются, радиус домена сильно уменьшается, и ЦМД попадает в зону радиальной неустойчивости. При H-H точки пересечения сливаются в точку касания с абсциссой Гк, которую называют радиусом коллапсирования. Значение Гк зависит от параметров материала.

Образец переходит в состояние устойчивого однородного намагничивания. Этот переход называют коллапсом ("реже - аннигиляцией) ЦМД. Для получения первоначальной лабиринтной структуры необходимо нагреть пластину выше точки Кюри или размагнитить ее специальными методами (§ 1.4).

Условия устойчивости, как следует из (1.171), определяются толщиной h и физическими свойствами материала пластины, в которой обеспечивается подобная структура.

Для характеристики совокупности физических свойств материала вводят понятие характеристической длины материала

Практический интерес представляет получение теоретическим путем значений внешнего иоля Явн, определяющих зону существования устойчивых ЦМД между границами эллиптической и радиальной неустойчивости для пластин с различными kfh. В [1.13] показано, что с уменьшением толщины пластины (с ростом УН) расширяется область полей устойчивого равновесия доменов (Ящах/Ятш возрастает от 1 до 1,7). В толстых пластинах незначительное колебание поля относительно Ящт может привести к коллапсу. Очень тонкие пластины (lo/hl) в ЦМД-технике не применяют из-за трудностей считывания информации (см. § 4.5). Соответствующие этим полям диаметры ЦМД для заданного материала составляют Dmta=£>K~4/o при lo=0,35h, Dmax~14/o при k=Q,2h.

В достаточно широком диапазоне изменения llh Dmax~3Dmin. С уменьшением толщины диапазон диаметров устойчивых доменов быстро растет. В реальных ЦМД-устройствах обычно обеспечивают DIh в пределах от 1,0 до 2,0.