Е. И. Кондорский показал, что для случая, описываемого уравнением (1.191), коэрцитивная сила определяется в основном градиентом внутренних напряжений и может быть представлена так:

Мгр / да \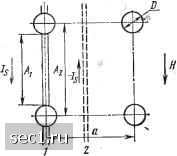

Рис. 1.42. Модель для определения коэрцитивной силы по теории включений

где бгр - толщина граничного слоя.

Теория Е. И. Кондорокого известна под названием теории напряжений. Она находит качественное подтверждение в материалах

с малым количеством включений, для которых характерно низкое значение коэрцитивной силы (магнитомягких материалов).

М. Керстен рассмотрел вопрос определения Не при большом количестве включений {теория включений).

Основные качественные положения этой теории состоят в следующем. Если считать, что в рассматриваемой модели значение отношения д\тр1дп мало (п -нормаль к поверхности стенки), т. е. угр?» const, то энергия £i,=YrpS будет тем меньше, чем меньше площадь стенки. Отсюда следует, что в отсутствие внешнего поля граница доменов стремится расположиться так, чтобы пересекать возможно большее число включений. Под воздействием внешнего поля граница может сойти с включений; ее площадь увеличится и соответственно возрастет Еу. Значение Не определяется максимальным увеличением граничной энергии при смещении границ доменов. Данные положения можно проиллюстрировать на примере простейшей модели, изображенной на рис. 1.42. В этой модели включения имеют форму сфер диаметром D, расположенных в виде кубической решетки с постоянной а. В отсутствие поля граница доменов располагается в положении /, которому соответствует наименьшая ее площадь. Под действием внешнего поля Я стенка смещается вправо, при этом площадь ее увеличивается в отношении (2Mi)2 и соответственно возрастает энергия Е-. Для рассматриваемой модели коэрцитивную силу можно определить по формуле

ТУ"

где /Сэф - эффективная постоянная магнитной анизотропии; р - концентрация примесей; п-показатель степени, равный 1, 7з, Vs и т. п; Pl - коэффициент, зависящий от отношения толщины граничного слоя к диаметру включений. При 6гр<С/ имеем Pi~6rp , а при бгр£> коэффициент pi=»Z)/6rp. Отсюда следует, что Не име-

ет наибольшее значение при дисперсности частиц D8rp. Из выражения (1.194) также следует, что Не растет с увеличением концентрации примесей §.

Существенное развитие теория включений получила благодаря работам Л. Нееля и Е. И. Кондорского, которые учли возможность образования на включениях магнитных зарядов и, следовательно, магнитостатическую энергию. Рис. 1.43 поясняет это положение. Для состояния, соответствующего рис. 1.43, а, магнитостатическая энергия

2 3

для состояния, соответствующего рис. 1.43, б,

=0,46.

Разность

Рис. 1.43. Зависимость магнитостатической энергии от положения граничного слоя:

а - граница вне включений; б - граница пересекает включения

(1.196)

энергий {Е-Е ) есть мера того поля, которое должно быть приложено для смещения доменной границы из положения рис. 1.43, а в положение рис. 1.43, б. Это поле необходимо учитывать при расчете коэрцитивной силы.

Возникновение магнитных зарядов вблизи включений приводит к образованию вторичной структуры доменов, характер которых зависит от многих причин: величины включений, свойств ферромагнетика (например, количества осей легкого намагничивания в нем) и др. Это хорошо видно из рис. 1.44, на котором изображена вторичная структура доменов

вблизи включений для некоторых типичных случаев. Магнитоста-тические взаимодействия в подобных образованиях могут быть рассчитаны.

Гистерезис, обусловленный необратимым процессом вращения.

Ранее было отмечено, что процессы вращения «в чистом виде» происходят в отсутствие доменных границ, поэтому исключается их смещение. Такие условия возможны, например, в очень мелких частицах ферромагнетика, для которых энергетически выгодно образование однодоменной структуры (см. § 1.7). Однодоменность предполагает отсутствие зародышей леремагничивания. Гистерезис, обусловленный необратимым процессом вращения, был впервые рассмотрен Н. С. Акуловым. Подход к решению данного вопроса можно проиллюстрировать на примере кривой намагничивания, представленной на рис. 1.40. Эта кривая имеет термодинамически неустойчивый участок FOG и устойчивые участки FEDO и GKLM. Значит, если магнитное состояние меняется, например, ло кривой CDEF,\o при достижении точки F (поля Я=-Яс) это состояние

изменится скачкообразно и будет соответствовать точке L. Аналогично при достижении по кривой MLKG точки G (поля Я=Яс) произойдет скачкообразный переход из точки G в точку D. Таким образом, магнитные свойства будут меняться по петле гистерезиса с коэрцитивной силой Яс. Используя уравнение (1.187), описывающее кривую рис. 1.40, при условии, что дН/д1=0 в точках F и G (Я=±Яс), получим

4 Kl Kl

с[1.о]=+ -~ 77-~ ± 777" • (1.197)

При намагничивании кристалла в направлениях, отличных от

[110], коэрцитивная сила определяется выражением, подобным (1.197), но с другими числовыми коэффициентами, т. е. в общем случае

1 (1.198)

til П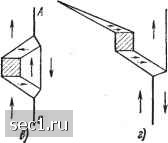

где 0,5а<2.

В расчете учитывалась только энергия кристаллографической анизотропии. Когда энергия, связанная с магнитоупругими напряжениями превалирует над другими видами энергии, можно получить выражение, аналогичное (1.198), заменив Ki произведением Kso:

(1.199)

Рис. 1.44. Вторичная структура ферромагнитных доменов вблизи включений (заштрихованные области) :

а - включение пересекается 180°-ным граничным слоем; б -• включение вне граничного слоя АВ; в - «прилипание» граничного слоя к включению; г - образование структуры шлейфа при сме-щенпи границ мея<ду доменами для ферромагнетика с тремя осями легкого намагничивания

коэффи-

где Ь= 1,5-4-3 - числовой циент.

Для полностью изотропного в магнитном отношении ферромагнетика коэрцитивная сила определяется только анизотропией формы частицы. Предположим, что частица имеет форму эллипсоида вращения и внешнее поле, обратное начальному направлению намагниченности, параллельно главной (длинной) оси. Тогда энергия

E=-L[HNaCos6+Ni sin2e)--[XoW,cos е, (1.200)

где Na - коэффициент размагничивания в направлении главной оси эллипсоида; Nb - коэффициент размагничивания в любом направлении, перпендикулярном главной оси; 0 -угол между векторами

Я и Is.