НЫХ элемента Fe, Ni, Co. Так, атом железа имеет структуру Is, 25, 2р, 3s2, Зрб, 3d, 4s, т. е. у него при не полностью заполненном слое 3d (6 электронов вместо 10 в соответствии с табл. 1.1) заполняется s-слой четвертой оболочки.

Момент количества движения электронной оболочки атома. Анализ экспериментальных данных по характеру взаимодействия между электронами в атоме показывает, что в большинстве случаев сила взаимодействия между спиновыми и орбитальными моментами всех электронов больше, чем сила взаимодействия между спиновым и орбитальным моментами каждого электрона. Такую связь называют связью Рассела-Саундерса. В этом случае полный момент количества движения электронной оболочки Pj определяют следующим образом. Складывая орбитальные моменты всех электронов атома, находят суммарный орбитальный момент Pi; складывая спиновые моменты, находят суммарный спиновый момент Ps.

Полный момент количества движения электронной оболочки

Py-Pi+Ps- (1-24)

Значения векторов Pi, Pg и Pj можно представить в следующем виде:

I Pi I /"ДГ+Тй; (1.25)

1 Ps I =VS{S + l)h; ;(1.26)

I Р = (/+1)Й, (1.27)

где L, S, J - квантовые числа, характеризующие соответствующие моменты.

Квантовое число L может иметь все целочисленные значения от суммы квантовых орбитальных чисел U для отдельных электронов, входящих в расчет, до их наименьшей алгебраической суммы. Например, в случае двух электронов с квантовыми числами h и tz возможны (при li>l2) следующие значения для L: h + k; li + k-v ...; h-h; всего 2I2+1 значений.

Квантовое число S для атома, содержащего электронов, может принимать следующие значения:

" --1;...; О при четном N,

2 2

; 1,...,-при нечетном N.

2 2 2

Квантовое число / принимает следующие значения: если L>S

J=L-{-S; L-{-S-l;...; L - S (всего 25 + 1 значений); если L<S, то

J=S-\L; 5+Z,-1;...; S-L (всего 2/,+ 1 значений).

МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОННОЙ ОБОЛОЧКИ АТОМА

Для определения полного магнитного момента необходимо найти его составляющие: суммарный спиновый магнитный ai о м е н т

I Ms I -2/5(5-f 1)(хд, (1.28)

суммарный орбитальный магнитный момент

i Mi I =1/"Д1+Т)1Хд (1.29)

Ей произвести их векторное суммирование:

M=Mi-fMs. (1.30)

Найденный таким образом магнитный момент М в силу гиромагнитной аномалии спина {gs= =2gL) не будет антипараллелен .

яолному механическому моменту Это иллюстрируется рис. 1.4, на котором масштабы выбраны так, что /Cl I Mi j = iiC21 Pi I; тогда /CiMs=iiC22Ps и M не лежит на одной прямой с Pj .

Составляющие Mi и Ms маг- Рис. 1.4. Сложение механических и шитного момента прецессируют во- магнитных моментов электронной обо-круг направления Pj *. При этом .

перпендикулярные к Р.г составляющие моментов в среднем по времени за период вращения равны нулю, ибо они непрерывно меняют свое направление, и полный магнитный момент Mj** электронной оболочки атома определяется только параллельными к Р.г составляющими моментов, т. е.

Mj=Mscos(Ps, Py)-}-7MiCos(Pi, Р); (1.31)

cos(P„ Р,)= S(S+l)+Jif + l)- LiL + ll . 32

2/S(S+1) (/+1) cosfP,. p., + l)+/(/ + l)-(+iI. (1.33)

Отсюда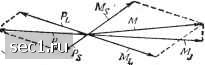

=gjVJ(J+ 1)-3 (1-34)

* в изолированном атоме, как в изолированной системе, вектор Pj=const МО значению и направлению.

** Полным магнитным моментом является М, а Mj представляет собой «оставляющую полного магнитного момента в направлении, параллельном Pj; sio поскольку среднее значение М за конечный промежуток времени равно Mj, •ffo его и называют полным магнитным моментом электронной оболочки.

* Отношение массы протона тп к массе электрона т известно с высокой точностью и равняется 1836±0,02.

называют фактором Ланде или g-фактором.

Для чисто орбитального момента 5=0,/=L, g-j=gi= 1; для чисто спинового L-0, S = J, gj=gs=2; в общем случае gj - дробное число, а при определенных соотношениях между L и S может быть равным нулю.

Векторы Pj и Mj подчиняются правилу пространственного квантования.

При этом следует отметить, что проекция

Mj=gjmjV-B .(1-36)

где mj-J; (/-1);...; (-/-Ы); (-/) не является целым числом, кратным Рв, поскольку gj в общем случае дробное число.

Определение полного магнитного момента атома существенно облегчается в связи с тем, что у заполненных слоев как орбитальные, так и спиновые магнитные моменты скомпенсированы. Поэтому при рассмотрении надо учитывать только не полностью заполненные слои.

Момент количества движения ядра. Атомное ядро состоит из Z положительно заряженных протонов, N нейтральных частиц-нейтронов и характеризуется массовым числом A=Z+N.

Различают нечетно-четные ядра, у которых нечетное А, нечетно-нечетные, у которых нечетные Z и N, и ядра с четным числом Z п N. Поскольку масса этих частиц* существенно больше массы электрона, то принято считать ядро относительно неподвижным, а его орбитальный механический момент количества движения - близким к нулю. Таким образом, механический момент количества движения ядра Pj определяется собственными (спиновыми) механическими моментами количества движения протонов и нейтронов. Экспериментально установлено, что спин нейтрона, так же как и протона, равен /2-

В соответствии с правилами квантования значения суммарного-момента количества движения ядра можно представить в следующем виде:

I РЛ =/7(7+1) .(1-37)

где / - спиновое квантовое число атомного ядра. Для ядер с четными Z и N 1-0; для нечетно-нечетных ядер / - целые числа; для; нечетно-четных ядер / - полуцелые числа.

Магнитный момент ядра. Магнитный момент ядра Mr обусловлен магнитными моментами сильно взаимодействующих, протонов и нейтронов.