и объемная магнитная восприимчивость

N,,0 С •

Н УЪкТ « Т \

где постоянная Кюри

(1-.70)

Формула (1.69) представляет собой закон Кюри [ср. с формулой (1.56)1.

При доказательстве закона Кюри были допущены следующие упрощения:

а) не учтены силы взаимодействия между элементарными носителями магнетизма парамагнетика (молекулярное магнитное поле);

б) не принято во внимание правило пространственного квантования.

Для учета влияния молекулярного магнитного поля Вейсс предложил считать это поле пропорциональным намагниченности, появившейся вследствие упорядоченности. Поэтому в парамагнетике действует поле

Язф=Я+«/, . (1.71)

где п - коэффициент пропорциональности.

Подставляя выражение для Яэф в формулу (1.68) и учитывая (1.69), получим

I=S-(H + nIy,

отсюда

н ~ т-пс ~ г-д •

где Д - постоянная Вейсса.

Выражение (1.72) представляет собой закон Кюри - Вейсса [ср. с формулой (1.57)].

Учет правила пространственного квантования сводится к тому, что угол В может принимать не любые значения, а лишь дискретный ряд возможных значений. В соответствии с этим при кванто-вомеханическом выводе формулы (см. например, [1.2]) парамагнитного момента, аналогичной формуле (1.67), интегрирование заменяется суммированием дискретных значений.

При этом выражение для магнитной восприимчивости принимает следующий вид: ,

. у=-. (i./o)

\ УЪкТ

сравнивая (1.73) и (1.69), находим, что постоянная Кюри

С=[.,£5У(У + 1). (1.74)

При рассмотрении магнитных свойств парамагнитных веществ следует также помнить о том, что, как указывалось (см. § 1.2), одновременно с парамагнетизмом обязательно имеет место и диамагнетизм. Поскольку эти эффекты обратны по знаку, суммарные магнитные свойства определяются их разностью; причем у большинства веществ парамагнетизм преобладает над диамагнетизмом.

Сравнение полученных формул с экспериментом показывает, что для парамагнитных газов и редкоземельных элементов, у которых парамагнетизм определяется магнитным моментом внутренних (недостроенных) слоев оболочек, слабо взаимодействующих между собой, свойства довольно точно отвечают закону Кюри; для парамагнитных металлов переходного ряда необходимо учитывать действие молекулярного поля. В некоторых случаях этому соответствует закон Кюри - Вейсса. Однако у некоторых парамагнетиков, например у многих солей железа, учет молекулярного поля путем введения поправки Д [см. формулу (1.72)] является недостаточным. В таких веществах поД действием поля кристалла возникает жесткая связь («замораживание») электронных орбит и под действием магнитного поля возможна ориентация только спиновых моментов. Свойства таких парамагнетиков не отвечают законам Кюри и Кюри- Вейсса.

Для некоторых металлов (например, щелочных), как отмеча-.лось, магнитная восприимчивость очень слабо зависит от температуры.

Я. Г. Дорфман в 1923 г. высказал предположение о том, что причиной парамагнетизма таких металлов являются в первую очередь электроны проводимости («электронный газ»). В дальнейшем эта гипотеза получила подтверждение в квантовомеханической теории парамагнетизма.

Теория парамагнетизма Ланжевена базируется на классической статистической физике; для объяснения явления парамагнетизма электронного газа необходимо обратиться к статистике Ферми.

Рассмотрим вопрос энергетического состояния системы при О К-По классической статистике О К Означает, что все частицы собрались в фазовой ячейке с нулевой энергией. По статистике Ферми это запрещено принципом Паули, который в применении к электронному газу можно сформулировать следующим образом: в фазовой ячейке, характеризующейся определенным значением кинетической энергии электрона, не может быть больше двух электронов с противоположно направленными спинами. Поэтому О К соответствует такое энергетическое состояние, при котором электроны наиболее плотно заполняют уровни с возможно меньшими значениями энергии.

При отсутствии магнитного поля плотность распределения спинов, направленных вверх и вниз, одинакова и имеет вид парабол (рис. 1.6, а).

Верхнюю границу энергии при таком распределении называют уровнем или энергией Ферми. При повышении температуры характер распределения изменяется, переходя при температуре окола 10 К, когда тепловая энергия сравняется с энергией Ферми, в классическое распределение Максвелла - Больцмана. Однако при температурах существования твердых тел распределение электронов по энергиям мало отличается от распределения при О К.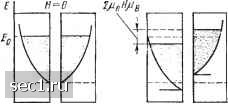

нф о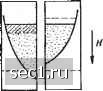

n(-i-e) n(-e)

Рис. 1.6. к объяснению парамагнетизма электронного газа

При отсутствии внешнего магнитного поля суммарный магнитный момент электронного газа равен нулю. При включении поля Н энергия электронов со спином, параллельным полю,- уменьшится на цвЦоЯ, а со спином, антипараллельным полю, увеличится на цвр-оЯ, и кривые сместятся так, как показано на рис. 1.6, б. Однако-такое состояние не отвечает минимуму энергии и является неустойчивым. Поэтому часть антипараллелъно направленных спинов перейдет в полосу с параллельными спинами, т. е. произойдет выравнивание уровней. В результате этого появится избыток электронов, с параллельной ориентацией спинов и возникнет магнитный момент, обусловленный парамагнетизмом электронного газа (рис, 1.6, в).

Парамагнитная восприимчивость электронного газа может быть представлена * как

2£п

(1.75>

где п - число электронов в единице объема; £о - энергия Ферми, Сравнение формулы (1-75) с формулой (1.69) для магнитной.

восприимчивости идеального парамагнетика показывает, что:

а) парамагнитная восприимчивость металлов (электронного

газа) в отличие от парамагнитной восприимчивости идеальных

* Вывод формулы (1.75) см., например, в [1.2].