случайных переменных Af;, /=1, 2, ... п, отсюда следует, что в области преобразования ФПВ Y является лг-кратной сверткой ФПВ от X,. Обычно л-кратную свёртку выполнить непосредственно более сложно, чем воспользоваться методом характеристической функции для нахождения распределения ФПВ для F, как описано выше.

Если мы имеем дело с /7-мерными случайными величинами, необходимо определить -мерные преобразования Фурье от СФПВ. В частности, если Х„ 2... /?, - случайные величины с ФПВ р {х , .х,,... х), п-мерная характеристическая функция определяется как

4r(jv,jv,...Jv„) = E

\ >-1

(2.1.81)

= Г...Г ехр jy.X, p{x,x,,...x„)dx,dx,...c/x„.

Специальный интерес представляет двухмерная характеристическая функция

v/(7v,, М)= Г Г e""V.Y„xOflfx-,rfY,. (2.1.82)

J со J-OQ

Заметим, что частные производные от \iU\,jV2) ™ и V2 можно использовать для получения совместных моментов. Например, легко видеть, что

(2.1.83)

Моменты более высоких порядков можно получить аналогичным образом.

2.1.4. Некоторые часто используемые распределения

В последующих главах мы встретим несколько различны.х типов случайньк величии. В этом разделе мы перечислим эти новые часто встречающиеся случайные величины, их ФПВ, ПФР и моменты. Мы начнё.м с биномж1льного распределения, которое является распределением дискретной стучайной величины, а з;1теы представил! р;1спределение некоторых непрерывных сл>1айных величин.

Бппомшипыюс распределение. Пусть .V - дискретшъ! cлJийн;u величина, которая принимает дв;1 возмолшых зн;1чения, например Л = 1 или Л =0, с вероятностью ри I - р соответственно. Соответствующая ФПВ для X пошшш! на рис. 2.1,6.

1-р р

Рис. 2.1.6. Функция распределения вероятностей А

Теперь предпололшм, что

где .V,, /=1;2.../7, - статистически независимые и идентично ргюпределенные cл>ulйныe величины с ФПВ, показанной на рис 2.1.6. Какош! функция распределения F?

Чтобы ответить на этот вопрос, заметим, что изначально Y - это ряд целых чисел от О до /; Вероятность того, что У=0, просто равна вероятности того, гго все А,=0. Так как У, статистически независимы, то

Р(У = 0) = (1-р)".

Вероятность того, что У=1, равна вероятности того, что одно слагаемое Х,=1, а остальные равны щто. Так как это событие может возни1снуть п различными путями,

Р(Г=1) = «Р(1-рГ.

Далее, вероятность того, что Y=k; равна вероятности того, что к значений Л,=1, а - к равна нулю. Так K.UC теперь имеется

к\(п-к)\

различны.ч комбинаций, которые приводят к результату {Y=k}, получаем

Р(У=А) = С*/(1-/Г, где С* - биномиальный коэффициент. Следовательно, ФПВ Y лгожно выразить так

Г/Л )\kj

Р(У)= ZPiY=kny-k)Z

t=0 кО

рЧ1-рГ*5(у-а-).

ИФР д.ги Y

Fiy) = P(Y<y)= Z

где [vj означает наибольшее целое ™сло ш, такое, чго ш <у.

ИФР (2.1.87) характеризует биномиальное распределение случайной величины. Первые два молсента К равны

£(У) = /1Р,

а характеристтеская функция

E(Y)-npil-p) + np\ ст- =пр(1-р).

(2.1.84) (2.1.85) (2.1.86) (2.1.87)

(2.1.88)

(2.1.89)

Равномерное распределение. ФПВ и ИФР равномерно распределенной случайной величины Л показаны на рис. 2.1.7.

P(-v)

ЩЬ-а)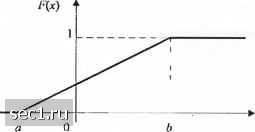

Рис. 2.1.7. Графики ФПВ и ИФР для равномерно распределенной случайной величины

Первые два момента .Нравны а хар;1ктеристическая функция равна

vy(yV) =

Mb - а)

(2.1.90)

(2.1.91)

Гауссовское распределение. ФПВ гауссовской или нормально распределенной случайной величины опреде.аяется формулой

где 1Пх - математическое ожидание, а - дисперсия случайной величины. ИФР равна

х-т.

V2na -i V7t V V2a J

где erf(r) - фунхсция ошибок, которая определяется выражением

erf(x) = 4-/oV. ФПВ и ПФР иллюстрир)10тся на рис. 2.1.8.

(2.1.92) (2 1 93) (2.1,94)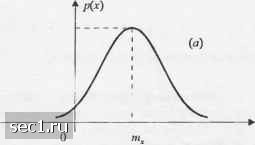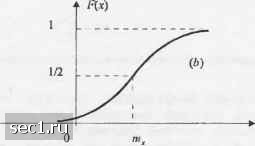

Рис. 2.1.8. Гр;1фики ФПВ (а) и ИФР (Ь) гауссовской случайной величины

ИФР F(x) можно та1сже выразить через дополнительную функцию ошибок, т.е.

ад = 1--егГс

erfc(x) = \ydt = l-erf(x). л/л

(2.1.95)

Заметим,™ erf (-х) =-erf (х). erfc(-x) = 2 - erfc(x), erf (0) = erfc(oo) = О и erf (оо) = erfc(O) = 1. Для jr >

m, дополнительная функция ошибок пропорциональна площади под частью гауссовской ФПВ. Дчя больши.ч течений Л дополнительная фушсция ошибок erf(ic) может быть аппроксимирована рядом

erfc(x) = -=

1-3 13-5

2х- 2-х

(2.1.96)

причем ошибк11 аппроксимации меньше, чем последнее удерживаемое слагаемое.

Функция, которая обычно используется для площади под частью гауссовской ФПВ, обозначается через Of г) и определяется как

2(x) = -j;e-V2. х>0.

Ср;шнивая (2.1.95) и (2.1.97), находим

0(x) = ierfc

\f2)

(2.1.97)

(2.1.98)

Характеристическая функция гауссовской случайной величины со средним шх и дисперсией равна

Центральные моменты гауссовской случайной величины равны

E[{X-mJ

l • 3 • (А - 1)а* (четные к) [о (нечетные А),

(2.1.99)

(2.1 100)