6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ

Качество оценки параметра сигнала обычно измеряется её смещением и дисперсией. Чтобы определить эти характеристики, предположим, что мы имеем последовательность

наблюдений

.v JCt л,

(6.5.1) что оценка

= х с ФПВ /;(хф), из которых извлекаем оценку параметра ф. Смещение оценки ф(х) определяется так:

смещение = е ф(х) - ф,

где ф - истинное значение параметра. Если /г ф(х) =ф, мы говорим несмещенная. Дисперсия оценки ф(х) определяется так:

а; = 1:{[ф(х)])-{4ф(х)]}. (6.5.2)

В общем трудно вычислить. Однако хорошо известным результатом в теории

оценивания параметра (см. Хелстром, 1968) является нижняя граница Крамера-Рао для среднеквадратической ошибки:

Т / [г

ф(x)]J/Alп/;(xф), \. (6.5.3)

Ф(х)-ф

>

-I I

Заметим, что если оценка несмещённая, то числитель в (6.5.3) равен единице, н граница (6.5.3) приводит к нижней границе для дисперсии а\ оценки ф(х), т.е.

о1>\1е- j\np[x ф) (6.5.4)

Поскольку 1п/;(х ф) отличается от логарифма отношения правдоподобия постоянным множителем, не зависящим от ф, то получим

п;;(хф)] = £1пЛ(ф)] j = - т1пЛ(ф)1 (6.5.5)

Следовательно, нижняя граница для дисперсии равна

a]>\lE

(6.5.6)

Эта нижняя граница-очень полезный результат. Она даёт оценку близости при сравнении дисперсии практической оценки относительно нижней границы. Несмещённая оценка, дисперсия которой достигает нижней границы, называется эффектнвнон.

В общем эффективные оценки являются редкими. Если они существуют, то являются оценками максимального правдоподобия. Хорошо известный результат из теории оценивания параметра - это то, что МП оценка параметра асимптотически (при произвольно большом числе наблюдений) не смещена и эффективна. В значительной степени эти желательные свойства определяют важность МП оценки параметра. Также известно, что МП оценка имеет асимптотически гауссовское распределение [со средним ф и дисперсией, равной нижней границе, определяемой (6.5.6)].

В случае МП оценок, описанных в этой главе для двух сигнальных параметров, дисперсии в общем обратно пропорциональны отношению сигнал-шум или, что эквивалентно, обратно пропорциональны мощности сигнала, умноженной на интервал наблюдения 7. Далее, дисперсии оценок, управляемых решениями, при малых вероятностях ошибки в целом ниже, чем дисперсии оценок, не управляемых решениями.

Фактически качество МП оценок, управляемых решениями, для фит достигает нижней границы.

Следующие примеры относятся к расчёту нижней границы Крамера-Рао для МП оценки фазы несущей.

Пример 6.5.1. МП оценка фазы немодулированной несущей, как было показано в (6.2.11), удовлетворяет условию

J г(/) sin(2я/:у + ф,)/ - О, (6 5.7)

/(/) = л(/;ф)+ /;(/) = со5(2л +ф) + н(/) . (6.5.8)

Условие (6.5.7) получено при взятии производной логарифма функции правдоподобия

аДф) = /М-/;Ф)/. (6.5.9)

Дисперсия ф имеет нижнюю границу

> -1

К NJ2T, ад

(6.5.10)

a-Tq~ \а- ~ \а-

Множитель \I2Tq- это эквивалентная (односторонняя) шумовая полоса идеального интегратора.

Из этого примера мы видим, что дисперсия МП оценки фазы имеет нижнюю границу

а: >1/у,, (6.5.11)

где у 1 - а" /2уУ„5,ц петлевое ОСШ. Это также дисперсия, получаемая при оценке фазы несущей посредством ФЗП с оценкой, управляемой решениями. Как мы уже видели, оценки, не управляемые решениями, нельзя выполнить так хорошо из-за потерь в нелинейностях, требуемых для снятия модуляции, например потерь из-за квадратирования или возведения в м-ю степень.

Похожие результаты можно получить для качества оценок параметра задержки, рассмотренных выше. В дополнение к их зависимости от ОСШ качество оценки параметра задержки является функцией от огибающей сигнального импульса. Например, на практике обычно используется импульс, имеющий спектр в виде приподнятого косинуса (см. разд. 9.2).

Для такого импульса среднеквадратическая ошибка (а) оценивания параметра

задержки как функция от ОСШ показана на рис. 6.5.1 для оценок, управляемых и не управляемых решениями.

Отметим значительное улучшение качества оценки, управляемой решениями, по сравнению с оценкой, не управляемой решениями Теперь, если меняется полоса частот импульса X, меняется огибающая импульса и, следовательно, среднеквадратическая ошибка оценки параметра задержки также меняется. Например, если меняется полоса частот импульса, который имеет спектр в форме приподнятого косинуса, среднеквадратическая ошибка меняется так, как показано на рис. 6.5.2. Заметим, что ошибка уменьшается по мере увеличения полосы частот импульса.

В заключение мы представили метод МП оценки сигнальных параметров и применили его для оценки фазы несущей и параметра задержки символов. Мы также описали их характеристики качества.

0,20

Оценивание, ue упрапляемае решениями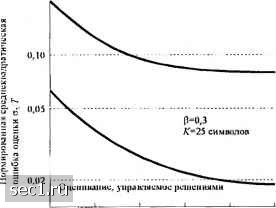

13 20

ОСШ (Ali)

Рис. 6-5.1. Качество оценки параметра задержки

дш фиксированного сигнала и фиксирошнпюй петлевой полосы [L.Frjnks, Syncluonizulion Subs) stem: Analysis and Design, 1983]

0.50

0,20

O.U)

0,05 -

0,02

Оцеп

. не ура[шяемое решениями

ОСШ=15д1; k=2i снмиолов

Оцеииаи1с. уирамясмис 1сшеия»м

О 0,1 U.2 0,3 0,4 0 5

Колншииипг::.нм1:. по nu.ioi:u чл:!»! 3 Пол.,1:.1-(1 + Г1) 27

Рис. 6.5 2. Качество оценки Шфаметра задержки

для i)HKCHiX)Baiuioro ОСШ и фиксированной петлевой полосы [L.Franks, Synciironizalion Subsy.slcnv Analysis and Design. 1983J

6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ

Восстановление несущей и фазовая синхронизация являются двумя темами, которые постоянно прорабатывались за последние три десятилетия. Петля Костаса была изобретена в 1956 г., а методы оценивания фазы, управляемого решениями, были описаны Прокисом и др. (1964) и Натали и Валбессером (1969). Работа по оценкам, управляемым решениями (ОСР), была мотивирована ранней работой Прайса (1962а,Ь). Всесторонний анализ фазо-замкнутой петли сначала появился в книгах Витерби (1966) и Гарднера (1979). Книги, которые охватывают вопросы восстановления фазы несущей и техники синхронизации, были написаны Стиффлером (1971), Линдсеем (1972), Линдсеем и Саймоном (1973), Мейром и .Лшайдом (1990) .

Определённое число учебных статей появилось в журналах IEEE по ФЗП и синхронизации символов. Мы цитировали для примера статью Гупта (1975), который рассматривает как аналоговую, так и цифровую реализацию ФЗП, и статью Лидсея и Чая (1981), которая посвящена анализу цифровых ФЗП. В дополнение учебная статья Френкса (1980) описывала методы оценки фазы несущей и синхронизации символов, включая методы, основанные на оценках по правилу максимального правдоподобия. Статья Френкса содержится в специальном исследовании в IEEE Transactions on Communications (август 1980), посвященном синхронизации. Статья Мюллера и Маллера (1976) описывала алгоритм цифровой обработки принимаемого сигнала для выделения синхроимпульсов.

Применение правила максимального правдоподобия для оценки параметра было впервые описано в контексте оценки радиолокационного параметра (дальность и скорость перемещения объекта). Впоследствии это оптимальное правило было применено как к оцениванию фазы несущей и параметра синхронизации, так и к совместному оцениванию этих параметров и самих данных. Статьи на эти темы были опубликованы различными исследователями, включая Фальконера (1976), Менгали (1977), Фальконера и Сальца (1977), Мейерса и Френкса (1980).

В этой области следует отметить работы В.Б. Ша.чгильдяна, А.А. Ляховкина, М.С. Лохвицкого 5(), 51], а также В.В. Гинзбурга и А.А. Каяцкаса [49] (прп).