ЗАДАЧИ

6.1. Докажите отношение (6.1.7).

6.2. Нарисуйте эквивалентную реализацию приемника дпя двоичны.\ сигна.10в ФМ (рис. 6.1.1), которая содерлсит согласованный фильтр вместо корре.чятора.

6.3. Допустим, что петлевой фильтр (см. (6.2.14)) для ФЗП имеет передаточную функцию

Gis) = -

a) Определите передаточную функцию H{s) дня замкнутой петли и укажите, является ли петля устойчивой.

b) Определите коэффициент зату.\ания и резонансную частоту петли.

6.4. Расслютрите ФЗП для оценки фазы несущей сигнала, дая которого петлевой фильтр задан так:

G(.)=-.

a) Определите передаточную функцию Я(у) для замкнутой пет.ли и ее усиление при / = О.

b) Дт1 какого диапазона значений т, и АГ петля устойчива?

6.5. Петлевой фильтр G{x) в ФЗП реа.шзован цепью, показанной на рис. Р6.5. Определите CHCTeMHjTO функцию G(.v) II выразите постоянные времени т, и т, через параметры цепи.

DliMl

Рнс. Р.б.5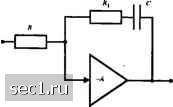

6.6. Петлевой фильтр G(.v) в ФЗП реализован активным фильтром, показанны1м на рис. Р.6.6. Определите системную фуншию G(.v) и выр<1зите постоянные времени через шфаметры цепи.

rtic pc 6

6.7. Поюг/ките, что син.хронизатор с окнами на задержку-опережение, поюгзанный на рис. 6.3.5, является близкой аппроксимацией системы син.\ронизации, ил.аюстрированной на рис. Р6.7.

6.8. Основываясь на правиле МП, определите метод оценки фазы несущей дтя двоичной людуляции с пассивной паузой.

6.9. При передаче и приеме сигналов между двигающимися объектами передаваемый сигнал получаст сдвиг частоты, прямо пропорциональный скорости перемещения. Так называемый доплеровский сдвиг

частоты, возникающий в этом случае, определяется формулой /д = ±-,

где и - скорость взаимного перемещения передатчика и приёмник:), X - длина волны, а знак зависит от направления (движение вперёд или назад) взаимного перемещения приёмник! и передатчик). Допустим, что в мобильно)! сотовой системе связи индивидуальный получатель перемещается со скоростью 10(J км/час относительно базовой станции. Узкополосный сигнал псредг)ётся на несущей 1 ГГц.

a) Определите доп.леровское смещение частоты.

b) Какова по.лоса отс.леживающей петли при доплеровски.\ сдвигах, если петля рассчитана на отслеживание доплеровски.\ сдвигов пользователей, двип1ющи,\ся со скоростями до 100 км/час?

c) Положим, что полоса переданного сигнала 2 МГц сосредоточена около 1 ГГц. Определите величину доплеровского рассеяния между вер.хней и нижней частями сигнала.

6.1(1. Покг)жите, что среднее значение МП оценки в (6.2.38) равно ф , т.е. что оцен1йа несмещённая.

6.11. Определите ФПВ МП оценки фазы в (6.2.38).

6.12. Определите МП оценку фазы дтя офсетной КФМ.

Согласованный фильтр

d/dl

Стробирующее

устройство

Стробирующе

устройство

sgn (•)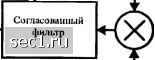

Рис. Рб.7

6.13. Однополосный сигнал AM можно представить так:

",„ (О = -Ккг it)coslnfj - §г {f)sin 2л/-,/], где Sri}) ~ преобразование Гильберта от gyif), а /1,„- уровень амплилды, который содержит ин(юрмацию

Покалчите математически, что петлю Костаса мояою использовать ддя де\юдуляции ОБП сигнала AM.

6.14. Информация передаётся квадратурной компонентой в системе связи посредством двоичной ФМ. TaiotM образом, принимаемый сигнал имеет вид

г(/) = ±у12Р cosilnf + ф) + .JlP sinilnf, + ф) + n{t),

где ф - фаза несущей, а n{l) - АБГШ. Немодулированная компонента нес> щей используется как. некий

сигнал на приёме д.1я оцениванш! фазы несущей.

a) Нарисуйте блок-счему приёмнию), включая оцениватель (1)азы несуще11.

b) Покалситс математичсс1си опергшии, определяющие оценивание (1)азы несущей ф ;

c) Выразите вероятность ошибки детектирования двоичного сигнала ФМ как фун1щию от суммарном переданной мощности Pj = F, + Р. Какова потеря качества, обусловленная концентрацией частоты переданной мощности в петле сигнала? Рассчитайте потерю при Р. / Pj- = 0,1.

6.15. Определите сигнальную и шумовую компоненты на в.ходе ФЗП (с возведением в четвёрт>ю степень (М-4)), используелюй для генерирования фазы несущей при демод.ищии КФМ. Игнорируя шулювыс

ко.\шоненты, кроме те.ч, которые линейно связаны с шумом n{f), определите дисперсию оценки (>азы выхода

ФЗП.

6.16. Вероятность ошибки делюдуляции и детектирования двоичной ФМ, если имеется ошибка в определении ()азы несущей на , равна

сох~

Предположите, ггo фазовая ошибю! от ФЗП дюделируется гауссовской случайной вслишной с нулевым средним и дисперсией ctJ «л" . Определите выражение дая средней вероятности ошибки (в интегрально.м виде).

ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И

КОДИРОВАНИЕ

в главе 5 мы обсуждали проблему цифровой модуляции Л/ = 2* сигналов, когда каждый сигнал содержит к бит информации. Мы видели, что некоторые методы модуляции обеспечивают лучшее качество, чем другие. В частности, мы показали, что ортогональный ансамбль сигналов позволяет нам сделать вероятность ошибки произвольно магюй, взяв число сигналов Л/оо при обеспечении ОСШ на бит у/, -1-6 дБ. Таким образом, мы можем оперировать с пропускной способностью канала с аддитивным белым гауссовским шумом в пределе, когда показатель расширения канала B. = fV/R-ca. Приходится платить высокую цену, поскольку растет экспоненциально с длиной блока к. Такое неэкономное использование полосы канала крайне нежелательно.

В этой и последующих главах мы рассмотрим сигналы, создаваемые посредством двоичных или недвоичных последовательностей. Результирующие сигналы, обычно, характеризуются показателем расширения полосы, который растет только линейно с к. Следовательно, кодированные сигналы предлагают в потенциале большую частотную эффективность, чем ортогональные М-позиционные сигналы. Мы увидим, что, в общем, кодированные сигналы предлагают преимущество качества не только в системах с ограничением мощности, когда R/W <1, но также в системах с ограничением полосы, когда R/W>\.

Мы начнём с установления нескольких моделей каналов, которые будут использованы для расчета выгоды канального кодирования, и мы хотим ввести концепцию пропускной способности канала для различных моделей канала. Затем мы будем обсуждать вопросы выбора (синтеза) кодов для эффективной связи.

7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ

Напомним, что в модели цифровой системы связи, описанной в разделе 1.1, передатчик содержит кодер канала, имеющий дискретный вход и дискретный выход, за которым следует модулятор. Функция дискретного кодера канала состоит во введении в двоичную информационную последовательность некоторой контролируемой избыточности, которую можно использовать в приёмнике для преодоления влияния шума и интерференции, возникающих при передаче сигнала по каналу. В общем процесс кодирования включает в себя взятие к информационных бит на определенном временном интервале и отображение каждой Л-битовой информационной последовательности в уникальную (взаимно однозначную) и-битовую последовательность, называемую кодовым словом. Величина избыточности, вводимая кодированием данных таким путем, измеряется отношением п1 к . Величину, обратную этому отношению, а именно kin, называют скоростью кода.

Двоичная последовательность выхода кодера канала питает модулятор, который служит интерфейсом к каналу связи. Как мы уже обсудили, модулятор может просто отобразить каждый двоичный символ в один из двух возможных сигналов, т.е. «О»