отображается сигналом st), а «1» отображается сигналом s-,{t). Альтернативно,-

модулятор может передавать д-битовые блоки за определенное время, используя М = 2 возможных сигналов.

На приёмной стороне цифровой системы связи демодулятор обрабатывает сигналы, искажённые каналом, и преобразует каждый принятый сигнал в скаляр или вектор, который представляет оценку переданных символов данных (двоичных или М-позиционных). Детектор, который следует за демодулятором, должен решить, передан «О» или «1». В этом случае детектор выносит жёсткое решение. Если мы посмотрим на процесс вьшесения детектором решения как на форму квантования, мы заметим, что жёсткое решение соответствует двоичному квантованию выхода демодулятора. В более общем виде .мы можем рассмотреть детектор, который квантует выход на 0>2 уровней, т.е. С-ичный детектор. Если используются М-позиционные сигналы, тогда 0> М. В экстремальном случае, когда вообще не производится квантования выхода демодулятора, О = оо. В случае, когда О > М, мы говорим, что детектор ъътосш.мягкое решение.

Квантованный выход детектора затем подаётся на канальный декодер, который использует имеющуюся в его распоряжении избыточность для коррекции искажений в канале.

В следующих разделах мы опишем три модели канала, которые будут использоваться для установления максимально возможной битовой скорости для канала.

7.1.1. Модели канала

В этом разделе мы опишем модели канала, которые будут полезны при синтезе кодов. Наиболее простая-это модель двоичного си.м.метричного канала (ДСК), которая соогветствует случаю, когда М = 2 , и жёсткому решению детектора.

Двоичный симметричный канал. Рассмотрим канал с аддитивным шумом, и пусть модулятор и демодулятор/детектор включены, как части канала.

Ихолныс

Вышиш .иншыс

-►

СоспшноП канал, .чнсьрстый но и.\илу н но иы\о.чу

Рис. 7.1.1. Составной канал, дискретный по входу и по выходу, образованный путём включения в него модулятора и демодулятора/детектора как частей канала

Если модулятор применяет двоичные сигналы, и детектор делает жёсткие решения, то составной канал, показанный на рис. 7.1.1, имеет на входе и выходе двоичную последовательность с дискретным временем. Такой составной канал характеризуется

набором X = о, l возможных входов, набором Y = о, l} возможных выходов и набором

>словных вероятностей возможных выходов при условии возможных входов. Если канальный шум и другие нарушения вызывают статистически независимые ошибки при передаче двоичной последовательности со средней вероятностью р, тогда

Чаще всего, говоря о декодировании декодером мягких решений детектора, имеют в виду, что Qco

(7.1.1)

p(y=q\xi) = p(y=\\x = o) = p, p(y=i\x=i) = p(y=o\x = o) = i-p.

Таким образом, мы свели каскадное соединение двоичного модулятора, канала и двоичного демодулятора и детектора в эквивалентный канал с дискретным временем, который представлен графом на рис. 7.1.2. Этот симметричный канал с двоичным входом и двоичным выходом обычно называют двоичным симметричным каналом (ДСК). Поскольку каждый выходной двоичный символ канала зависит только от соответствующего входного двоичного символа, мы говорим, что этот канал без памяти.

Вход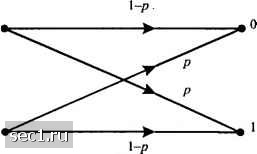

Выход

Рис. 7.1.2. Двоичный симметричный канал

Дискретные каналы без памяти. ДСК является частным случаем более общего канала с дискретным входом и дискретным выходом. Предположим, что входом кодера канала

являются -ичные символы, т.е. Л= Хо,д:,,...,х , , а выходом детектора являются

Q-ичные символы, где Q> М = 2. Если канал и модуляция без памяти, тогда

характеристика вход-выход составного канала, показанного на рис. 7.1.1, описывается рядом из qQ условных вероятностей

P(Y = y,\X = Xj)P(y,\x), (7.1.2)

где i = 0,1,Q-1 и j 0,1, ...,q-\. Такой канал называется дискретным каналом без памяти (ДКБП) и его графическое представление показано на рис. 7.1.3. Таким образом, если входом ДКБП является последовательность из п символов ц.и,,.-,",,. выбираемых из алфавита X, и соответствующим выходом является последовательность и,, и,,и, символов из алфавита У, то совместные условные вероятности определяются так:

Р{У, = х„У2 = х2,-Х = ,.\=и„Х,щ,...,Х„ = и„)11Р(У=У,\Х = щ) (7.1.3)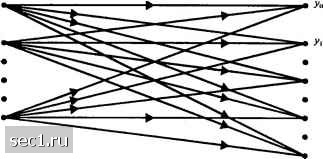

Уо I

Рис. 7.1.3. Дискретный канал, д-ичныИ по входу и (2-ичный по выходу

Это выражение - просто математическая констатация условия отсутствия памяти.

В общем, условные вероятности {P(y,\Xj)}, которые характеризуют ДКБП, могут быть

упорядочены в форме матрицы Р = где, по определению, р, = Piy.lXj) . Р называется

матрицей переходных вероятностей канала.

Канал с дискретным входом и непрерывным выходом. Теперь предположим, что на вход модулятора подаются символы, выбираемые из конечного и дискретного входного алфавита Л= {jCq, х,,х.,}, а выход детектора не квантован {Q = co). Тогда входом

декодера канала можно считать любую величину на вещественной оси, т.е. У = {-оо.оз}. Это ведет нас к определению составного канала без памяти с дискретным временем, который характеризуется дискретным входом X, непрерывным выходом Y и рядом условных ФПВ р(у\Хх,), k = 0,\,...,q-l.

Наиболее важный канал этого типа-это канал с аддитивным белым гауссовским шумом (АБГШ), для которого

Y=X + G, (7.1.4)

где G - гауссовские случайные величины с нулевым средним и дисперсией а, а X = х, = 0,1,-1. Для данного X = х следует, что Y является гауссовской случайной величиной со средним х и дисперсией ст. Это значит

р(у\Хх,) = -1с . (7.1.5)

Для любой входной последовательности X,, / = 0,1,...,и имеется соответствующая выходная последовательность

Y,=X, + G„ / = 1,2,(7.1.6) Условие, что канал без памяти, можно выразить так:

Сигнальные каналы. Мы можем отделить модулятор и демодулятор от физического канала и рассмотреть модель канала, в котором входы и выходы являются сигналами. Предположим, что такой канал имеет заданную полосу частот fV с идеальной частотной

характеристикой с(/) = 1 внутри полосы W, а сигнал на его выходе искажен аддитивным белым гауссовским шумом. Предположим, что x{t) является частотно-ограниченным входом для этого канала, а y{t) - соответствующий выход. Тогда

y{t) = x{t) + nit), (7.1.8)

где n{t) представляет реализацию аддитивного шумового случайного процесса. Подходящий метод для определения ряда вероятностей, которые характеризуют канал, -это разложить x{t), y{t) и n{t) в полный ряд ортонормированных функций. Это значит, мы выражаем х(г), y{t) и n{t) в форме

At) = i:y.M x{t) = Y.M; «(/) = ЕчУ;(0, (7.1.9)

I i I

где [х,}, {у,}и ряд коэффициентов в соответствующих выражениях, например