у, = \}{t)f:it)dt =\[x{t) + rit)]f;{t)dt =x, +«,. (7.1.10)

функции {f,U)] образуют полный ортонормированный ансамбль на интервале (0,г),

т.е.

где 5, - дельта-функция Кронекера. Поскольку гауссовский шум белый, то в выражениях

(7.1.9) можно использовать любой полный ансамбль ортонормированных функций.

Теперь используем коэффициенты в указанных выражениях для характеристики канала. Поскольку у, = , + > где и, - гауссовские случайные величины, то следует

Р(>,к) = ;;е , / = 1,2.... (7.1.12)

Поскольку функции {/(0} в разложениях являются ортонормированными, то следует, что {и;} некоррелированы. Поскольку они гауссовские, они также статистически независимы. Следовательно,

р{У1,У2-Уы\х1,Х2,-,х) = У1р(У/\х,) (7.1.13)

для любого N. Таким образом, описание сигналов канала сведено к эквивалентному каналу с дискретным временем, характеризуемым совместной ФПВ, даваемой (7.1. 1*2).

Когда аддитивный шум белый и гауссовский со спектральной плотностью {jVq, дисперсия -2N0 для всех / в (7.1.12). В этом случае отсчёты x{t) и y(t) можно брать со скоростью Найквиста 2W отсчетов/с так, что х = x{i/2W) и х = y[i/2w). Поскольку шум

белый, отсчёты шума статистически независимы. Таким образом, (7.1.12) и (7.1.13) описывают статистику отсчётов сигналов. Заметим, что на временном интервале длительностью Г имеются Л = 2Тотсчетов. Этот параметр используется ниже для получения пропускной способности частотно-ограниченного канала с АБГШ.

Выбор модели канала для его использования на определенном временном интервале зависит от объекта исследования. Если мы интересуемся синтезом и анализом качества кодера и декодера дискретного канала, приемлемо рассмотреть модели канала, в которых модулятор и демодулятор являются частью составного канала. С другой стороны, если наша цель - синтез и анализ качества цифрового модулятора и цифрового демодулятора, мы используем модель сигнального канала.

7.1.2. Пропускная способность канала

Теперь рассмотрим ДКБП с входным алфавитом = {X(,,jr,,...,x ,} и выходным алфавитом Y= {yo,yi,...,yQ i}ii рядом переходных вероятностей PiylXj), определённых в (7.1.2). Предположим, что передан символ Xj, а принят символ у. Взаимная информация о событии X = Xj, когда имеет место собьггие ¥ = У;, равно \og[P(y,\Xj)/Р(у)], где

P{y,h Р(У = У) = Z РМр(у<1к)- (7114)

21* 323

Следовательно, средняя взаимная информация, получаемая по выходу У о входе X, равна

"/- Q-

l(;y) = llllP{My.\jyog Р(у.\х)/Р(у) . (7.1.15)

j-0 1=0 *

Характеристики канала определяют переходные вероятности Р(у\х), но вероятности входных символов определяются дискретным кодером канала. Величина I(X;Y), максимизируемая по набору вероятностей входных символов P(Xj) является величиной, которая зависит только от характеристик ДКБП через условные вероятности Р(у,\х). Эта

величина названа пропускной способностью канала и обозначается С. Таким образом, пропускная способность ДКБП определяется так

C = max/(X;y) = maxXXi(JJ,)logfp(:,xJ/p(;.,)]. (7.1.16) Максимизация l{X; У) выполняется при условиях

Размерность С - бит/символ, если берется логарифм с основанием 2, и нат/символ, если берётся логарифм с основанием е. Если символы поступают в канал каждые секунд, то пропускная способность канала в единицу времени в бит/с и нат/с равна С/т, = С .

Пример 7.1-1

Для ДСК с переходными вероятностями

P(0/l)=P(l/0) = ;;

средняя взаимная информация максимизируется, если входные вероятности Р(0) = P(l) = 4. .Следовательно, пропускная способность ДСК равна

C = ;7log2p + (l-p)log2(l-;?) = l-(;7), (7.1.17)

где н{р) - двоичная энтропийная функции. Кривая для С в зависимости от р иллюстрируется на рис. 7.1.4. Заметим, что при р = 0 пропускная способность равна 1 бит/символ. С другой стороны, при р=2 взаимная информация между выходом и входом равна 0. Следовательно, пропускная способность равна 0. При j<p<\ мы можем поменять местами на входе ДСК О и 1, так что С оказывается симметричной функцией относительно точки p = j.

В нашей трактовке двоичной модуляции и демодуляции, данной в главе 5, мы показали, что р является монотонной функцией от отношения сигнал-шз (ОСШ), как показано на рис. 7.1.5(a). Следовательно, когда С строится как функция ОСШ, она возрастает монотонно по мере увеличения ОСШ. Зависимость С от ОСШ иллюстрируется на рис. 7.1.5(b).

Далее рассмотрим канал без памяти с АБГШ и дискретным временем, описываемый переходными ФПВ, определяемыми (7.1.5). Средняя максимальная взаимная информация между дискретным входом X = {xq,xj,...,x i} и выходом У={-оо,оо} определяется

пропускной способностью канала в бит/символ и равна

4-1 «>

(7.1.18)

(7.1.19)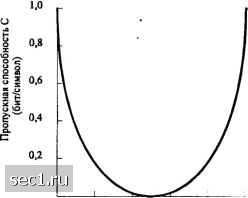

о 0.2 0.4 0,6 0.8 1.0 Вероятность ошибки, р

Рис. 7.1.4. Пропускная способность ДСК как функция вероятности ошибки р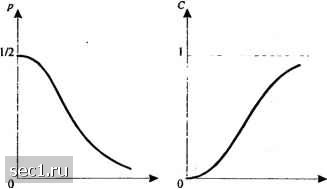

(а) (Ь)

Рис. 7.1.5. Общее поведение вероятности ошибки и пропускной способности канала, как функции от отношения сигнал/шум (ОСШ)

Пример 7.1.2

Рассмотрим канал без памяти с АБГШ и с возможными входами X = А и X --А. Средняя взаимная информация 1{Х;¥) максимизируется, если вероятности входов Р{Х = А)-Р{Х = -A) = j. Следовательно, пропускная способность такого канала в бит/символ равна

C = fip(y\A)log,dy+i ]p(y\-A)iog2dy. (7.1.20) Рис. 7.1.6 иллюстрирует С как функцию отношения A/la.