Интересно отметить, что в двух моделях канала, описанных выше, выбор одинаковой вероятности для входных символов максимизирует среднюю взаимную информацию. Таким образом, пропускная способность канала получается, когда входные символы равновероятны. Однако, такое решение для пропускной способности канала, даваемое формулами (7.1.16) и (7.1.17), не всегда имеет место.

-20 -12 +4

101g(/(W)UB)

Рис. 7.1.6. Пропускная способность как функция ОСШ (AVla) для канала без памяти с АБГШ и двоичным входом

Ничего нельзя сказать в общем относительно задания вероятностей входа, которые максимизируют среднюю взаимную информацию. Однако, в двух моделях канала, рассмотренных выше, переходные вероятности канала проявляют форму симметрии, которая влияет на максимум I{X;Y), который получается, когда символы входа равновероятны. Условия симметрии можно выразить через элементы матрицы переходных вероятностей Р канала. Когда каждая строка этой матрицы является перестановкой других строк и каждый столбец является перестановкой других столбцов, матрица переходных вероятностей симметрична, а входные символы с равной вероятностью максимизируют

I{X;Y).

В общем необходимые и достаточные условия для совокупности вероятностей входных символов {P{Xj)), при которых максимизируется I{X;Y) и, следовательно, достигается пропускная способность ДСК, таковы (задача 7.1):

/(х;У<С для всех j с p(x]>0,

i[x;,y) = C для всех j с p[x) = Q, (7.1.21)

где С - пропускная способность канала, и

/(,;>)Ui.)log. (7.1.22)

Обычно относительно просто проверить, удовлетворяет ли совокупность входных символов с равными вероятностями условиям (7.1.21). Если они не удовлетворяются, то ряд входных символов с неравными вероятностями {P(Xj)) могут удовлетворять (7.1.21).

Теперь рассмотрим ограниченный по полосе частот канал с аддитивным белым гауссовским шумом. Формально, пропускная способность такого канала в единицу времени определена Шенноном (1948) так:

с = lim max l(X; Y), (7.1.23)

7-»«> p(x) i

где усреднённая взаимная информация определена (3.2.17). Альтернативно, мы можем использовать отсчёты или коэффициенты >,, х,} и {и,} в ряде разложений x{t),y{t) и n{t) соответственно для определения средней взаимной информации между Хд, =[х,Х2...х,/] и yj =[уу2...у\,тяе NIWT, у, =х,+у, и piy,\Xj) определены (7.1.12). Средняя взаимная информация между х, и уд, для канала с АБГШ равна

/(x„;y,)= ...Я...Ыу»1»)1084*»*« =

- " , , (7.1.24)

Максимум i{X:Y) по входной ФПВ получается, когда входы х,} статистически независимые гауссовские случайные величины с нулевыми средними, т.е.

д/2лст7

где ст - дисперсия каждого х,. Затем из (7.1.24) следует, что

ax/(x;Yj = Xilog[l + lvf,

= Nlog

= Hriog

(7.1.26)

(7.1.27)

Предположим, что мы накладываем ограничение на среднюю мощность входных сигналов x{t), т.е.

Следовательно,

TP Р

Подставив этот результат в (7.1.27) для а", получаем

f Р \

max/(x;Yj = riogl +

(7.1.28)

(7.1.29)

(7.1.30)

В заключение можно получить пропускную способность канала в единицу времени путем деления результата (7.1.30) на Т. Таким образом,

C = Wlog

(7.1.31)

Это базовая формула для пропускной способности частотно-ограниченного канала с АБГШ с частотно-ограниченным и ограниченным по средней мощности входом. Она была впервые получена Шенноном (1946).

График пропускной способности (бит/с), нормированной к полосе W, как функция от отношения средних мощностей сигнала /Jp и шума WN, дан на рис. 7.1.7.

Заметим, что пропускная способность увеличивается монотонно с увеличением ОСШ. Таким образом, при фиксированной полосе пропускная способность канала увеличивается

с увеличением переданной мощности сигнала. С другой стороны, если фиксирована, пропускную способность можно увеличить за счёт увеличения полосы W.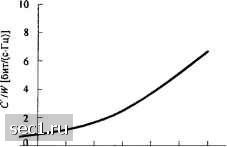

о 4 8 12

10 \ziPJWN,)

16 20

Рис. 7.1.7. Нормированная пропускная

способность канала как функция ОСШ для ограниченного по полосе частот канала с АБГШ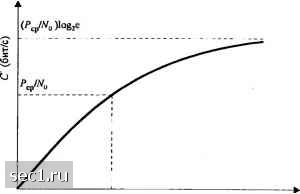

Рис. 7.1.8. Пропускная способность канала как функция полосы частот при фиксированной средней мощности сигнала

Рис. 7.1.8 дает зависимость С от W. Заметим, что если W становится неограниченной, пропускная способность канала приближается к предельной величине

C = log,e = .

(7.1.32)

Поучительно выразить нормированную пропускную способность канала CjW как функцию от ОСШ на бит. Поскольку Р представляет среднюю мощность (в Ваттах), а С

определено в бит/символ, то следует

Р = С%, (7.1.33)

где - энергия сигнала на бит. Следовательно, (7.1.31) можно выразить так:

W N,

Следовательно,

% 2-1 C/W

Когда С/Ж=1, /"0 = 1 (О дБ). При C/f->oo

" C/W

«exp(ln2-ln).

(7.1.34)

(7.1.35)

(7.1.36)

Таким образом, Щ/Nq растёт экспоненциально, когда C/W->оо. С другой стороны, когда C/JV-O,

которое равно -1,6 дБ. Зависимость C/W от Щ,/ Nq показана на рис. 5.2.17.

Итак, мы получили выражение для пропускной способности для трех важных моделей канала, которые рассматриваются в этой книге. Первая - это модель канала с дискретными входом и выходом, для которой ДСК частный случай. Вторая, с дискретным входом и непрерьшным выходом, - это модель канала без памяти с АБГШ. При помощи этих двух