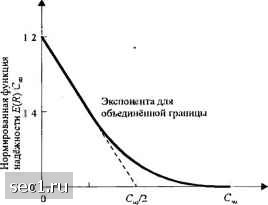Скорое!ь передачи Л (би\/с)

Рис. 7.1.9. функция надёиоюсти канала с АБГШ при неофаниченной полосе частот

Хотя вероятность ошибки можно сделать как угодно малой увеличивая число ортогональных или биортогональных или симплексных сигналов при R < С„ , для относительно умеренного числа сигналов, имеется большое расхождение между реальным качеством и лучшим достижимым качеством, даваемой формулой для пропускной способности канала. Для примера, из рис. 5.2.17 мы видим, что ансамбль из М=1б ортогональных сигналов требует для достижения вероятности ошибки - 10" ОСШ на бит при когерентном детектировании примерно 7,5 дБ. В контрасте формула для пропускной способности канала указывает на то, что для С/Ж = 0,5 надёжная передача возможна с ОСШ порядка -0,8 дБ. Это представляет большую разницу в 8,3 дБ/бит н является стимулом для поиска более эффективных форм сигналов. В этой главе и главе 8 мы покажем, что кодированные сигналы могут значительно сократить расхождение.

Аналогичные расхождения в качестве существуют также в частотно - ограниченной области рис. 5.2.17, где R/W> 1. Однако, в этой области мы должны быть более искусны для того, чтобы использовать кодирование для улучшения качества, поскольку мы не можем расширить полосу частот, как в области с ограничением мощности сигнала. Польза от техники кодирования для эффективных по полосе частот систем связи также обсуждается в главе 8.

7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ

Синтез систем кодированной модуляции для эффективной передачи информации можно разделить на два базовых подхода.

Один - это алгебраический подход, который первоначально касался синтеза техники кодирования и декодирования для специального класса кодов, такие как циклические блоковые коды и свёрточные коды. Второй подход является вероятностным и он касается анализа качества общего класса кодированных сигналов. Этот подход даёт границы для вероятности ошибки, которые можно достичь для связи по каналу с некоторыми специфическими характеристиками.

В этом разделе мы ознакомимся с вероятностным подходом к кодированной модуляции. Алгебраический подход, базирующийся на блоковых и сверхточных кодах, рассматривается в главе 8.

-» ч

7.2.1. Случайное кодирование, основанное на использовании ансамбля из Л/двоичных кодовых слов

Рассмотрим ансамбль из М кодовых слов, образованных из /-мерных двоичных кодовых слов вида

С,=[с„с„...б,„], /-1,2,...,М, (7.2.1)

где =0 или 1. Каждый символ кодового слова отображается двоичным ФМ сигналом, так что сигналы, соответствующие кодовому слову С, можно выразить так:

•;W = Z-V/.W / = 1,2,...,М. (7 2.2)

1, ecлиc=l,

ecлиc=0 -

II i - энергия на кодовый символ. Таким образом, сигналы .v(/) эквивалентны -мepным векторам

S. =

л;з ....s;„ , / = 1,2,...,М , (7.2.4)

которые соответствуют верщинам гиперкуба в 77-мерном пространстве.

Теперь предположим, что информационная скорость на входе кодера равна R бит/с и мы кодируем блоки из к бит на определенном временном интервале У посредством одного из Л/сигналов. Следовательно, k-RT и требуется AY 2 -2" сигналов. Удобно определить параметр D следующим образом:

Z) = -измер./с (7.2.5)

Таким образом, /7 = DT-это размерность пространства сигналов.

Гиперкуб имеет 2" - 2° вершин, из которых М - 2" могут быть использованы для передачи информации. Если мы навяжем условие D>R, то часть вершин, которые мы используем как сигнальные точки, равна

Р-- = -"- (7.2.6)

Ясно, если D> R, имеем F-> О, когда Тсо.

Вопрос, который мы хотим ставить, следующий. Можно ли выбрать подмножество М = 2 вершин из 2" = 2° имеющихся в распоряжении вершин так, чтобы вероятность ошибки при 7->оо или, что эквивалентно, когда ->эо? Поскольку часть /

используемых вершин приближается к нулю, когда 7->оо, возможно выбрать А/ сигналов, имеющих минимальное расстояние, которое увеличивается, когда У->йо и. следовательно, РО.

Вместо того, чтобы пытаться найти простой ансамбль из М кодовых сигналов, для

которых мы рассчитаем вероятность ошибки, рассмотрим ансамбль из (2")* различных

пугей, по которым мы можем выбрать М вершин из 2" имеющихся в распоряжении вершин гиперкуба. С каждым из 2 выборов мы можем связать систему связи, содержащей модулятор, канал и демодулятор, которые оптимальны для выбранного

набора из М сигналов. Таким образом, имеется 2" систем связи, одна для каждого выбора М кодовых сигналов, как показано на рис. 7.2.1. Каждая система связи характеризуется своей вероятностью ошибки.

Входная последовательность

Модулятор

Мод\лягор

{.v,(0)«

"(О

Рис. 7.2.1. Ансамбль 2"систем свлт. Кюкда i система выбирает

одну из 2*" возможных последошггельностсй из .\/сигналов

Предположим, что наш выбор М кодовых сигналов основан на случайном выборе из множества 2" возможных ансамблей кодов. Таким образом, случайный выбор т-го кода, обозначенного {л;} , происходит с вероятностью

(7.2.7)

и соответствующую условную вероятность ошибки для этого выбора кодовых сигналов обозначим ) Тогда средняя вероятность ошибки по всему набору кодов

ш=1 ш=\

где верхняя черта над означает усреднение по ансамблю кодов.

Ясно, что некоторые выборы кодов приведут к большим вероятностям ошибки Например, код, который сопоставит все М к -битовых последовательностей одну и ту же вершину гиперкуба приведет к очень большой вероятности ошибки. В таком случае

P({5,}J>P. Однако, будут так же выборы кодов, для которых P([y,}J < У. Следовательно, если мы получим верхнюю границу для эта граница будет так же справедлива для тех кодов, для которых Р{л;} J<P. Далее, если 7.-0 при Уоо,