тогда мы можем делать заключение, что для этих кодов ({-5;}) -> О, когда Г -> оо.

Для того, чтобы определить верхнюю границу для Р, рассмотрим передачу -битового сообщения Х= XiX.-.x, , где Xj = 0 или 1 для j-\,2,...,k. Условная вероятность ошибки, усредненная по ансамблям кодов, равна

(7.2.9)

всешды

где /X,{.jj-условная вероятность ошибки Л-битового сообщения Х, которое

передается посредством кода (-sj. Для т-го кода вероятность ошибки iXj,(ji}j имеет верхнюю границу

.(Х,. {5,} J < 2 J. (7.2.10)

где i„(s,, s.) - вероятность ошибки для двоичной системы связи, которая использует сигнальные векторы и для передачи одного из двух равновероятных Л-битовых сообщений. Таким образом.

(7.2.11)

Меняя порядок суммирования в (7.2.11), получаем

S2(s;,s,). (7.2.12)

где i(s„s.) представляет среднюю по ансамблю вероятность y„(s„s), полученную усреднением по 2" кодам или по 2* системам связи.

Для канала с АБГШ вероятность ошибки двоичной системы /„(s,, s) равна

V2AoJ

(7.2.13)

где dj = - s. . Если s, и отличаются no d координатам, то

dl=b,-kf-jl[ s) =d(2yle;) =4dfS,. (7.2.14)

Следовательно,

(7.2.15)

Теперь мы можем усреднить i,(s„s) по ансамблю кодов. Поскольку все коды равновероятны, сигнальный вектор s, с равной вероятностью может соответствовать любой из 2" возможных вершин гиперкуба, и это имеет место статистически независимо

от соответствия любой вершины сигнальному вектору . Следовательно, p{s,, = s = 2 и

p{s Ф - \ независимо для всех / = 1, 2, и. Как следствие, вероятность того, что s, и различаются в d позициях, равна

Pd)A-\ , . (7.2.16)

Таким образом, математическое ожидание /*2шансамблю кодов можно выразить так:

\2dn

1 "fri

2 d-o\"y

Ц No J

(7.2.17)

Результат (7.2.17) можно упростить, если воспользоваться верхней границей для Q-функции

2dfS.

N0 J

<е

Таким образом.

P(s„s,)<2-"Z о-""" <2-"(l + e-/») <к(1 + е-*/0Г- (7-2.18)

Мы видим, что правая часть (7.2.18) не зависит от индексов I и к. Следовательно, если мы подставим границу (7.2.18) в (7.2.12), то получим

- м -

Р.М S РгМ = Ш-l)[i(l + e-/»)]" < M[i(l + е--)

Наконец, безусловную среднюю вероятность ошибки Ре получим усреднением Plt) по всем к -битовым информационным последовательностям. Таким образом,

= ХФОФ.) < 4i(l + e--")]"Z Ф.) = Mi(l + е-/-)]" (7-2.19)

it к

Этот результат можно выразить в более удобной форме, прежде всего определив параметр 7, который называется предельной скоростью и имеет размерность бит/измерение

Ро = log2, . - 1 - log. (1 + е-"«). (7.2.20)

M-f-e-

Тогда (7.2.19) можно записать в виде

<М2- =22-°. Поскольку п = DT, то (7.2.21) можно выразить так

Зависимость параметра как функции от / N показана на рис. 7.2.2. Видно, что О< 7 < 1. Следовательно, Р, -> О, Т-со, если информационная скорость 7?<D7.

(7.2.21) (7.2.22)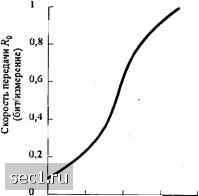

-10 -5 О

г,/Ла(дВ)

Рис. 7.2.2. Предельная скорость передачи / как функция ОСШ на измерение в децибела.к

Альтернативно (7.2.21) можно выразить так:

;2-"(»-° (7.2.23)

Отношение RID также имеет размерность

бит/измерение и может быть определено так:

R R RT к R = - = -7 =-= -. (7.2.24)

Таким образом, Л - это скорость кода, и 7<2-"°-* (7.2.25)

Мы замечаем, что, когда < У, средняя вероятность ошибки О, когда длина кодового блока и 00. Поскольку среднюю величину вероятности ошибки можно сделать произвольно малой при 00, отсюда следует, что существуют коды в ансамбле 2" кодов, которые имеют вероятность ошибки не больше, чем .

Из определения средней вероятности ошибки, данного выше, мы заключаем, что хорошие коды существуют. Хотя мы нормально не можем выбрать коды случайно, интересно рассмотреть вопрос о том, может ли случайно выбранный код быть хорошим. Действительно, можно легко показать, что в ансамбле имеется много хороших кодов. Сначала заметим, что Р - это средняя по ансамблю вероятность ошибки, полученная усреднением по всем, кодам и что все отдельные вероятности, очевидно, положительные величины. Если код выбран случайно, вероятность того, что его вероятность ошибки Р>аР, меньше, чем 1/а. Следовательно, не больше, чем 10 процентов кодов имеет вероятность ошибки, которая превосходит ХОР и не больше, чем 1 процент кодов имеют вероятность ошибки, которая превосходит \00Р.

Мы хотим подчеркнуть, что коды с вероятностью ошибки, превосходящей Р, не является обязательно плохими кодами. Например, предположим, что среднюю вероятность ошибки Р < 10~° можно получить, используя коды с размерностью /7,,, когда R>R. Тогда, если мы выберем код с вероятностью ошибки 1000Р<10~, мы можем скомпенсировать это увеличение вероятности ошибки увеличением длины кода п от 77„ до п = \ОпП. Таким образом, скромным увеличением размерности мы имеем код с

Р, < 10"°. Суммируя скажем, хороших кодов в изобилии и, следовательно, их можно легко найти даже случайным выбором.

Также интересно выразить среднюю вероятность ошибки в (7.2.25) через ОСШ на бит Yj. Чтобы это сделать, выразим энергию кодового сигнала так:

ёЩк\. П.2.26)

Следовательно, п = к%1\. Также заметим, что ЛД./-1. Таким образом, (7.2.25) можно выразить так:

Р < 2"*"" J (7 2 27)

где Yg - параметр, определяющей нормирование ОСШ, и равный

:C*"l-log,(l + r)

(7.2.28)

22-56