-5 О

10 ;г4(дБ)

Рис. 7.2.3. HiMoiM фаница для ОСШ на бит Д.ЧЯ двоичны.к противопололчны.ч сигна.юв

Теперь заметим, что -» О, когда к -<х> при условии, что ОСШ на бит Уь>у„. Зависимость Уо от КУь показана на рис. 7.2.3.

Заметим, что когда Rjb. Уц~21п2 Следовательно, вероятность ошибки для М двоичных кодовых сигналов эквивалентна вероятности ошибки, полученной из объединенной границы для М-ичных ортогональных сигналов, предполагая, что размерность кодового сигнала достаточно велика, так что Yo «21п2.

Параметр размерности D, который мы ввели в (7.2.5), пропорционален полосе канала, требуемой для передачи сигналов. Напомним, что согласно теореме отсчетов, сигнал с полосой W можно представить отсчётами, взятыми со скоростью 2W отсчётов/с. Таким образом, на временном интервале 7 имеется п = 2WT отсчётов или, что эквивалентно, имеем степеней свободы (размерность). Следовательно. D можно приравнять 2W. В заключение заметим, что двоичные кодовые сигналы, рассмотренные в этом разделе, используются, когда ОСШ на измерение мало, например, й;/Л„<10. Однако, когда <fJN„> 10, величина асимптотически приближается к 1 бит/измерение. Поскольку скорость кода ограничена так, что она меньше то двоичные кодовые сигналы получаются неэффективными при %./N>\0. В этом случае мы можем использовать недвоичные кодовые сигналы для того, чтобы достичь увеличение числа бит на измерение. Например, многоуровневый кодовый ансамбль можно синтезировать из недвоичных кодов путем отражения калсдого кодового элемента в один из возможных уровней (как в AM). Такие коды рассматриваются ниже.

7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами

Вместо того, чтобы синтезировать двоичные кодовые сигналы, предположим, что мы используем недвоичные коды с кодовыми словами вида (7.2.1), где кодовые элементы с,

выбираются из ансамбля (О, 1,/-1} . Каждый кодовый элемент отображается в одно из ({ возможных значений амплитуд. Таким образом, мы синтезируем сигналы, соответствующие/7-мерным векторам (s,.), как в (7.2.4), где компоненты выбираются

из ряда амплитуд, принимающих cj возможных значений. Мы имеем cf возможных

сигналов. Из них мы выбираем Л/= 2" сигналов для передачи -битовых информационных блоков. Величины q амплитуд, соответствующих кодовым элементам

{О, \, (J-\}, обозначим {а,, ••• " будем предполагать, что они выбираются с

вероятностями {/;,}. Предполагается, что уровни амплитуд равномерно распределены на

интервале [-д/л/]- примера, рис. 7.2.4 иллюстрирует значения амплитуд при

Рис. 7.2.4. Сигншьный ал(1>авнт, состоящий из 4 уровней а\1плит>ды

В общем, соседние уровни амплитуд разделены интервалом 2ф]/((/-\). Такое задание гарантирует не только то, что каждая компонента ограничена пиковой энергией

, но также и то, что каждое кодовое слово ограничено по средней энергии, удовлетворяющей условию

Ы<"К- (7.2.29)

Путем повторения подхода, данного выше, для случайного выбора кодов в канале с АБГШ, находим, что средняя вероятность ошибки ограничена сверху

7 < Ml""" = 2" 2""" = 2 "", (7.2.30)

где li,, определено как

V/=i III 1

(7.2.31)

ci,-a,„, /,/."=1,2,.....,7 (7.2.32)

В частном случае, когда все уровни амплитуд равновероятны,

Р, =р.„ = 1ч,

и (7.2.31) сводится к

ll,=-\oJ±±p,p,.,e]. (7.2.33)

/=1 ,„=1 J

Для примера, когда q-1 и я, = а-, = д/Ч., имеем t/,, = t/„ = О, с/,, -1/,, - 2d

и,следовательно,

что совпадает с нашим прежним результатом. Когда (J-4, я, --/Х . "= = -Л/з. «4 = А. имеем „„„ = 0 для /J7=l, 2,3,4, d.d2djrd. ,=d.,-=d, -JKP d,- d,-d., t/,,= 4-y 3 и t/, -2y[&. . Следовательно,

" 2 + 3e-""» +2e--"-"" +e""" " "

Ясно, 7, теперь насыщается до 2 бит/измерение по мере увеличения elN. График как функции /Л при равноотстоящих и равномерно распределённых уровнях амплитуд показан на рис. 7.2.5 для </ = 2,3,4,8,16,32 и 64. Заметим, что таким образом, для больших ОСШ -> о, когда /; -> оо при условии, что R < DR„ = 2И7, бит/с.

Если мы изменим пиковую энергию элемента, но сохраним заданную среднюю энергию на кодовое слово, как дано в (7 2 29), возможно получить большую верхнюю границу на число бит/измерение. Для этого случая, результат, полученный Шенноном (1959b), равен

22* 339

- 1 +

log2e + -log2

(7.2.35)

График в функции от ОСШ на измерение (/Ло) также дан на рис. 7.2.5 Ясно, что наш выбор равномерно отстоящих, равновероятных уровней амплитуд, который приводит к Rq, является субоптимальным. Однако, эти кодовые сигналы легче синтезировать и реализовать на практике. Это важное преимущество, которое оправдывает их использование.

10,0 6,0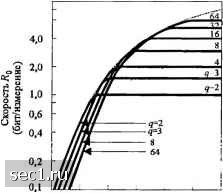

-10 о 10 20 30 40 50 Энергетическое отношение на измерение 101g(gyAJ

Рис. 7.2.5. Предельная скорость Rg для равноотстоящих уровней амплитуды с равными вероятностями

7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ

Пропускная способность частотно-ограниченного канала с АБГШ с заданной средней мощностью входного сигнала было приведена в разделе 7.1.2 и определяется так:

С = Wlog,

бит/с.

(7.2.36)

где - средняя мощность входного сигнала, а. W- полоса канала. Интересно выразить

пропускную способность этого канала в бит/измерение, а среднюю мощность в энергии/измерении. С учётом того, что D = 2W и

имеем

P.,=jK=DK- (7.2.37)

Определив С„ - С /2W= СID и заменив W w Р в (7.2.36), можно записать

C. = log,

1 + 2

- rlog2(l + 27?<.Yb) бит/измерение.

(7.2.38)

Это выражение для нормированной пропускной способности канала можно сравнить с R, как показано на рис. 7.2.6. Поскольку С„- безусловный верхний предел скорости передачи RJD, то R<C„, как и ожидалось. Мы также видим, что для малых значений %INq разница меду R и С„ приближенно равно 3 дБ. Следовательно, использование