а обычные моменты можно выразить через центральные моменты

Сумма и статистически независимых гауссовских случайных величин таюке является гауссовской случайной величиной. Чтобы это продемонстриров;1ть, предпололсим

Y = X,, (2.1.102)

где Л„ /=1,2. .я - независимые случайные величины со средними т, и дисперсиями аД Используя результат (2 1.79), мы находим, что характеристическая функция К равна

1=1 1-1

--Z- (2.1.104)

.=: f-i

Следовательно, У является гауссовской случайной величиной со средним ту и дисперсией а у.

Хн-квадрат-ряспредслеппе. Случайная величина с хи-квадрат-распределением порождается гауссовской cлyийнoй величиной, в том смысле, то ее формирование можно рассматривать как преобразование последней. Для конкретности, пусть Y = Х~, где А - гауссовсюш случайная величина. Тогда Y имеет хи-квадрат-распределение. Мы различаем два вида хи-квадрат распределения. Первое шпывается центральным хи-квадрат-распределением, и получается, когда X имеет нулевое среднее значение. Второе нашвается нецентральным хи-квадрат-распределением, и получаете», когда X имеет ненулевое среднее значение.

Сначала рассмотрим центральное хи-квадрат-распределение. Пусть А - гауссовская случайная величинл с нулевым средним и дисперсией а. Поскольку YX, результат даётся функцией (2.1.47) с параметрами а=\ и 6=0. Таким образом, получаем ФПВ Y в виде

Pr{y)-lt-°\ y>Q. (2.1.105)

V27t>CT

ИФР для г

iV(y) = loV(«)=loe "du, (2.1.106)

которое не может быть выражено в замкнутом виде. Характеристически! функция, однако, может быть выражена в замкнутой форме:

V0V) = 7--ш- (2.1.107)

(l-y2va2J

Теперь предположим, что случайная величина Y определяется как

Y = Y.X}, (2.1.108)

где Л„ /=1, 2, ..../7, - статистически независимые и один.1ково распределенные гауссовские случайные величины с нулевыми средними и дисперсией а. Вследствие статистической независимости X, характеристическая функция Y

riP) = -f-4wr- (21109)

Обратное преобразование этой харахсгеристической функции дает ФПВ

где Г(р) - гамма-функция, определённая как

r(p) = lt--dt,p>0,

ip) = (Р-ТУ-.Р- целое число, ;з > О, (2.1.111)

Эта ФПВ является обобщением (2.1 105) и названа хи-квадрат- {или гамма-) ФПВ с п степенями свободы. Она иллюстрируется рис. 2.1.9.

Случай, когда п=2, определяет экспоненциальное распределение. Первые два момента У равны

ИФР У равна

£(y) = 2/7a+«V, al=2n<j\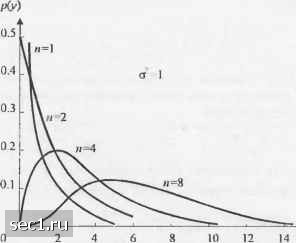

> У

(2.1.112)

(2.1.113)

Рис. 2.1.9 Графики ФПВ для случайной величины с хи-квадрат-распределением дги нескольких значений степеней свободы

Этот интеграл преобразуется к неполной гамма-функции, которая была табулирована Пирсоном (1965) Если п четно, интеграл (2.11.113) можно выразить в з;1мкн\том виде.

В частности, пусть m = -jr«, где т - целое. Тогл1, использ>я повторно интефирование по частям. ПОЛ) чаем

t о А!

,У = 0.

(2.1.114)

Теперь рассмотрим нецентральное хи-квадрат-распределение. которое яамется результатом возведения в квадрат гауссовской случайной величины с нен)левым средним. Если X - гауссовская случайная величина со средним шх и дисперсией а", случайная величина У=А~ имеет ФПВ

, y>0.

(2.1.115)

Этот результат получается при использокшии (2.1.47) дтя гауссовской ФПВ с распределением (2.1.92). Характеристическая функция для ФПВ

Тг(» = -

(2.1.116)

(1-J2..T

Дчя обобщения результатов предположим, что У является суммой 1свадр;1тов гауссовских случайных величин, определенных (2.1.108). Все Х,. / = 1.2,...,«, предполагаются статистичесы! независимыми со

средними и/,, / = 1,2,...,w, и одинаковыми дисперсия\п1 а. Тогда характеристическая фун1сцил, пол)ч;1сма* из (2.1.116), при использовании соотношения (2.1.79) равна

-ехр

сгерр

Обратное преобразование Фурье от этой характеристической функции даёт ФПВ

а- J

где введено обозначение

(2.1.117)

(2.1.118)

(2.1.119)

а 1о.{х) -модифицироашная функция Бесселя первого рода лорядта а, которую люжно представить бесконечным рядом

(л:/2)*-*

к ок\Т{(х+к+\)

х>0.

(2.1.120)

ФПВ, определяемая (2.1.118), называется нецентральным хи-квадрат-распределением с п степенями свобооы. Параметр 5" назван параметром нецеитральиости распределения. ИФР дпя нецентрального хи-1свадрат-распределения с п степенями свободы

(it-2, 4

е 112 1 VM

du .

(2.1.121)

Этот интефал не выражается в замкнутой форме. Однако, если т = п - целое число, ИФР можно выразить через обобщённую 0-функцию Маркума, которая определяется клк

= а(.,Ь)н-е(-- 2 1 /,(«*),

(2.1.122)

к=.\\а

Qiia.b) = е"(°* У (- 1к(аЬ), Ь>а>0 (2.1.123)

Если заменить переменную интегрирования и в (1.2.121) на х, причём =и/а" , и пололшть, что a=s/a, тогда можно легко найти

5 у[у

а а

(2.1.124)

В заключение заметим, что первые два момента д.1я центрального хи-1свадрат-распределения случайных величин равны

EiY) = nG+s-, =2na*+4aV.

(2.1.125)

Релесвскос распределение. Релеевское распределение часто используется как модель для статистики сигналов, переданных через радиоканалы, таких как, например, в сотовой радиосвязи. Это распределение тесно связано с центральным хи-квадр;1т-распреде.лением. Чтобы это проиллюстрировать, положим, что )=.Vi"+A2, где Л и .\; - статистически независимые гауссовские случайные величины с нулевыми средни.ми и одинаковой дисперсией а. Из изложенного выше следует, чго Y имеет хи-1свадрат-распределение с двзмя степенями свободы. Следовательно, ФПВ для Y

Рг(У) =

1

Теперь предположим, что мы определяем новую случайную величину

RX{+Xi =4y . .

(2.1.126) (2.1.127)