случайно выбираемых, оптимально ограниченных по усреднённой мощности многоуровневых сигналов приводит к функции скорости 7, которая находится внутри 3 дБ зоны пропускной способности канала. Требуется тщательно разработанная техника определения границ, чтобы показать, что вероятность ощибки можно сделать сколь угодно малой, когда R < DC = 2WC = С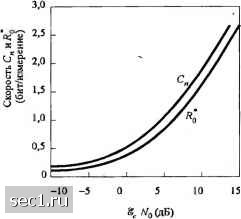

Рис. 7.2.6. Сравнение предельной скорости Л*

с пропускной способностью для кана.ла с АБГШ

7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ

В предыдущем обсуждении мы характеризовали качество кодирования и модуляции через вероятность ошибки, которая конечно является определяющей при синтезе системы связи. Однако, во многих случаях, расчет вероятности ошибки чрезвычайно сложен, особенно, если при обработке сигнала в приёмнике используются нелинейные операции, такие, например, как квантование сигнала, или когда аддитивный шум не гауссовский.

Вместо того, чтобы стремиться к расчету точных значений вероятности ошибки для специальных кодов, мы можем использовать усредненную по ансамблю среднюю вероятность ошибки при случайном выборе кодовых слов. Предполагается, что канал имеет CJ входных символов {0,1,...,-!} и О выходных символов (О, 1, 1} и

характеризуется переходными вероятностями где j = 0,1, I и

/ = 0,1,О-1, причем Q>q. Входные символы появляются с вероятностями {р} и

считаются статистически независимыми. Дополнительно, шум в канале считается независимым во времени, так что нет зависимости между принимаемыми соседними символами. При этих условиях, среднюю вероятность ошибки по ансамблю при случайном выборе кодовых слов можно получить с использованием границы Чернова (см. Витерби и Омура, 1979).

Общий результат, который получен для дискретных каналов без памяти, таков:

где п - длина кодового блока, R - информационная скорость в битах/с, D ~ число измерений в секунду, а 7 - предельная скорость для квантователя с О уровнями,

определяемая так:

Rq = max-j [Pj]

i-i)

7-1

(7.3.2)

С точки зрения синтеза кода, комбинация из модулятора, канала и демодулятора образует канал с дискретным временем с ij входами и О выходами. Переходные вероятности {P(i\j)} зависят от характеристик канального шума, числа уровней квантования и типа квантователя, например, равномерного или неравномерного. Для примера, в канале с АБГШ и двоичным входом, условное распределение выхода коррелятора в точке отсчета можно выразить так:

pb>\J)--f=-""""\ ./ = 0,1. (7.3.3)

где .

Wo = -1%, пц = д/ и а- = Л„.

Эти две ФПВ показаны на рис. 7.3.1. Рисунок также иллюстрирует схему квантования, которая разделяет вещественную ось на пять областей. При таком разделении мы можем вычислить переходные вероятности и оптимальным образом выбрать пороги, при которых деление на области происходит так, что максимизируется при заданном О. Имеем

р(ут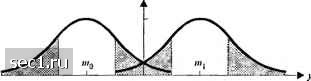

©00®©

Рис. 7.3.1. Пример квантования вы.\од21 демодулятора пятью уровнями

Pi\J) = lp{ymdy. (7.3.4)

где интеграл от р(у /) вычисляется по области /., которая соответствует переходной вероятности p{i jj.

Величина скорости R в пределе, когда О-со, определяет предельную скорость для

неквантованного выхода демодулятора или согласованного фильтра. Можно непосредственно показать, что, когда О -> «з, первое суммирование (сумма от / = О до 0-\) в (7.3.2) заменяется интегрированием, а переходные вероятности заменяются соответствующими ФПВ. Таким образом, когда канал состоит из q дискретных входов и одного непрерывного выхода у, который представляет неквантованный выход согласованного фильтра или коррелятора в системе связи, которая использует ФМ или многоуровневую (AM) модуляцию, предельная скорость определяется так

Ra = max

(7.3.5)

где 0< j<q-\ определяет вероятность передачи j-vo символа, a p{yу] - условная

плотность вероятности выхода у согласованного фильтра или взаимокоррелятора, когда передан у-й сигнал. Это и есть выражение для определения качества неквантованного декодирования (декодирования мягких решений).

Пример 7.3.1

Сравним качество двоичной AM в канале с АБГШ, когда приёмник квантует выход на () = 2, 4 и 8 уровней. Чтобы упростить проблему оптимизации при квантовании сигнала на выходе демодулятора, квантованные уровни располагаются в точках О, ±т,,, ±2т,,, ... ±(2*" - i)t;,, где t,, - параметр, определяющий шаг квантования, который должен быть

выбран, а /» - число бит, определяющие уровни квантования. Хорошая стратегия для выбора т,, - выбрать его так, чтобы минимизировать ОСШ на бит у,, которые требуются для работы с кодовой скоростью . Это значит, что параметр шага квантования должен оптимизироваться для любого ОСШ, что означает при практической реализации приёмника, что ОСШ должен измеряться. К сожалению, т,, не проявляет высокую чувствительность к малым изменениям в ОСШ, так что возможно оптимизировать т,, для определенного значения ОСШ и получать хорошее качество для широкой области ОСШ вблизи этого номинального значения, используя фиксированное т,.

Основываясь на таком подходе, выражение для Rq, определяемое (7.3.2), было пересчитано для h -1 (декодирование жестких решений), 2 и 3 бита, соответствующие числу уровней квантования 0 = 2, 4 и 8. Результаты даны кривыми на рис. 7.3.2. Величина Р„ для неквантованного декодирования мягких решений, полученная расчетом по (7.3.5), также дана на рис. 7.3.2. Видим, что двухбитовое квантование с т,, = 1 выигрывает около 1,4 дБ относительно декодирования жестких решений, а трехбитовое квантование с х,, = =0,5 дает дополнительное улучшение на 0,4 дБ.

При трёхбитовом квантовании мы проигрьшаем не более, чем на 0,2 дБ, относительно предельного неквантованного декодирования мягких решений. Ясно, что в будущем можно будет лишь немного выиграть путем улучшения точности обработки.

Если используется недвоичный код совместно с М-ичными (Л/ = cf) сигналами, принимаемый сигнал на выходе М согласованных фильтров можно представить вектором у = \ у Уп -Ум]- Предельная скорость для этого канала с М-ичным входом и М-ичным (неквантованным) выходом равна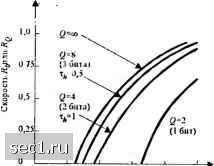

U 1 2 3 4 5

U Ш II.IU1IT, 7(Ali]

Рис. 7.3.2. Влияние laiiumiuiinHH iei иомсхнусюйчипосчь

кодоиой сисигмы сиям при iiix:i(c.ibiioii i:Ki)X)i;m или при двоищщи ФМ 11 hiUKijiL- с ASITU

Rq = max Ы

-log2 TjUPjp.J 1 VPiy\j)P(y\Ody

j-O I ЛЗ

(7.3.6)

где p{y j) - условная ФПВ вектора у на выходе демодуляторов при передаче/-го сигнала.

Заметим, что (7.3.6) похоже по форме на (7.3.5), за исключением того, что теперь мы имеем при обработке А/-мерный интеграл, поскольку имеется М выходов демодуляторов.