предположим, что М сигналов ортогональны, так что М выходов, обусловленных частными входными сигналами, статистически независимы. Как следствие,

pb\j) = Ps.n(ydWpXy) (7.3.7)

где Р,+„{Уд - ФПВ выхода согласованного фильтра, соответствующего переданному сигналу с номером j, а [р„{у)) определяется сигналами на выходах остальных согласованных фильтров. Если (7.3.7) подставить в (7.3.6), мы получаем

-log;

Л/-1

Hp] + SSml Jyylp.Mpiy)

j=0 jQ i=0

(7.3.8)

Максимизация no набору вероятностей входных сигналов приводит к = 1/ М для 1 < j < М. Следовательно, (7.3.8) ведет к

= log2

1 + (М-1)

.4P..Sy)Pniy)dy

(7.3.9)

= log,M-log,-l + (M-l)

4Ps.n{y)P.,iy)dy

Это - искомый результат для предельной скорости для канала с М-ичным входом и М -ичным векторным неквантованным выходом.

При когерентном детектировании М-ичных ортогональных сигналов соответствующие ФПВ равны

(7.3.10)

,- -е

где m = -J и а"=Лд. Подставив эти соотношения в (7.3.9) и вычислив интеграл, получим

, = Iog3

= log2

1 + (М-1)е

(7.3.11)

1 + (М-1)е-

где <S - энергия принимаемого сигнала, - информационная скорость в битах/сигнал, а Yft =ь/оОСШнабит.

Подчеркнём, что параметр скорости Я включает в себя кодовую скорость Я. Для примера если М = 2 и код двоичный то Я = Я. В более общем случае, если код двоичный и М = 2\ тогда Л/-ичные сигналы содержат Я = v/? бит информации. Также интересно заметить, что если код двоичный и М = 2 , тогда (7.3.11) преобразуется к Г 2 ]

К=ёг ~л -!гсУь2 М = 2 (ортогональных сигнала), (7.3.12)

что на 3 дБ хуже, чем предельная скорость для противоположных сигналов. Если положим в (7.3.11) Я и выполним решение относительно у,, то получим

(7.3.13)

Зависимость от Уь Для некоторых значений М иллюстрируется на рис. 7.3.3. Заметим, что кривые насыщаются для любых значениях М при = logj М

Интересно также рассмотреть предельную форму (7.3.11) при М ->со. Получаем

lim Rq = ТТГТТ, бит/сигнал. (7.3.14)

2NAn2

Поскольку iS = Р Т, где Т- длительность сигнала, то следует

и 1 2 3 4 5 б 7 ОСШ па бит, Y4 (дБ)

Рис. 7.3.3. Требуемое ОСШ на бит для работы с предельной скоростью Л, при использовании М-ичных ортогональных сигналов и когерентного детектирования в канале с АБГШ

Ьт - =

M-iua J

2Ы„\п2

(7.3.15)

Таким образом, при М ->оо предельная скорость равна половине пропускной способности канала с АБГШ с неограниченной полосой. Альтернативно, подставляя d = Rj-f, в (7.3.14) даёт Yj = 21n2 (1,4 дБ), что является минимальным значением ОСШ, требуемым для работы со скоростью R, когда М -> оо. Таким образом, при работе со скоростью R, требуется на 3 дБ больше мощности, чем предел Шеннона.

Величина R, определённая (7.3.11), базируется на использовании М ортогональных сигналов, которые субоптимальны, когда М мало. Если мы попытаемся максимизировать 7, путём выбора наилучшего ансамбля из М сигналов, то не будем удивлены, когда найдём, что оптимальным является ансамбль симплексных сигналов. Действительно, 7, для этих оптимальных сигналов определяется так:

(7.3.16)

1 + (М-1)е--» Если сравним это выражение с (7.3.11), то заметим, что 7 в (7.3.16) просто отражает тот факт, что ансамбль симплексных сигналов энергетически более эффективен в М/{М-1) раз.

в случае некогерентного детектирования ФПВ, соответствующая сумме сигнал + шум и одному шуму, можно выразить так:

Рп(у)-у

где, по определению а - -sj2<§i Nq . Расчёт даваемый (7.3.9), не ведёт к замкнутой

форме решения. Вместо этого можно интеграл в (7.3.9) рассчитать численно. Результаты для этого случая были даны Джорданом (1966) и Бухером (1980). Дпя примера, нормированная предельная скорость 7 для М-ичных ортогональных сигналов при некогерентном детектировании дана на рис. 7.3.4 для М - 2,4,8 и 16.

1.0 г

0.75 .

3 0.5 L-

0 25 -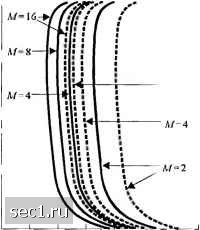

5 10

осш на бит, (дБ)

Рис. 7.3.4. Требуемое ОСШ на бит д-вд работы с предельной скоростью У при использовании Л/-ичны.\ ортогошшьны.ч сигналов и некогерентного детектирования в канале с АБГШ

С целью сравнения мы также дали кривые для предельной скорости при декодировании мягких решений (Q = М) для Л/-ичных сигналов. В этом случае имеем

л/0-л/) + л/(Л-1)Л/

0=М, (7.3.18)

где Яд; - вероятность ошибки символа. Для относительно широкого диапазона скоростей, разница между декодированием мягких и жёстких решений составляет приблизительно 2 дБ.

Наиболее удивительное в характеристиках качества, отображённых на рис. 7.3.4, - это то, что здесь имеется оптимальная скорость кода при малом М. В отличие от когерентного детектирования, когда ОСШ на бит уменьшается монотонно с уменьшением скорости кода, ОСШ на бит при некогерентном детектировании достигает минимума вблизи нормированной скорости 0,5 и увеличивается как при большей, так и при меньшей скоростях. Минимум довольно широкий, так что здесь имеется область скоростей от 0.2 до 0,9, где ОСШ на бит имеет минимум с разбросом до 1 дБ. Такое характерное поведение характеристики качества при некогерентном детектировании объясняется нелинейной характеристикой детектора.