7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ

Основополагающая работа по описанию канала в терминах его пропускной способности и случайного кодирования принадлежит Шеннону (1948а, Ь, 1949). Дополнительный вклад был впоследствии сделан Гильбертом (1952), Элиасом (1955), Галлагером (1965), Вайнером (1965), Шенноном и др. (1967), Форни (1968) и Витерби (1969). Все эти ранние публикации собраны в IEEE Press book под заголовком Key Papers in the Development of Information Theory под редакцией Слепяна (1974).

Использование параметра предельной скорости в качестве критерия синтеза было предложено и разработано Возенкрафтом и Кеннеди (1966) и Возенкрафтом и Джекобсом (1965). Он был использован Дмсорданом (1966) при синтезе кодированных сигналов для Л-ичных ортогональных сигналов с когерентным и некогерентным детектированием. Следуя этим основополагающим работам, предельная скорость была широко использована в качестве критерия синтеза кодовых сигналов для множества различных условий в канале.

ЗАДАЧИ

7.1. Покажите, что следующие два отношения являются необходимыми и достаточными условиями ил* ансамбля входны.\ вероятностей {Р(х)}, чтобы максимизировать i(x:y) и, таким образом, достичь

пропускной способности ДКБП:

i{x;y)<C для всех j с р(ху)>0,

l(xj ;y)=C для всех j с p(xj=О, где С - пропускная способность канала и

7.2. Рис. Р.7.2 иллюстрирует Л/-ичный симметр№1ный ДКБП с переходными вероятностялш Р(у\х) = \-р, когда х=у = к,для к = 0,1,2,...,М -1. и Р(у\х) = р/(М -1), когда х*у.

a) Покажите, что этот канал удовлетворяет условиям, данным в задаче 7.1, когда P(xi)-l/М .

b) Определите и постройте зависимость пропускной способности канала от р.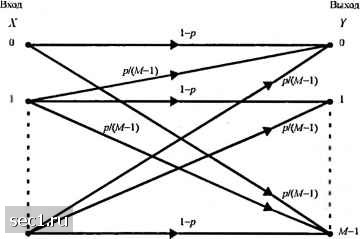

Рис. р.7.2

7.3. Определите пропускные способности каналов, показанных на рис. Р.7.3.

7.4. Рассмотрите два канала с переходными вероятностями, покапанными на рис. Р.7.4. Определите, достигается ли максимизация скорости передачи по каналу при равной вероятности входных символов.

7.5. Телефонный канал имеет полосу частот IV = 3000 Гц и отношение мощностей сигнала и шума 400 (26 дБ). Предположим, что мы характеризуем канал, как частотно-ограниченный канал с АБГШ с

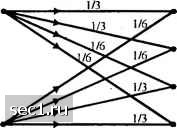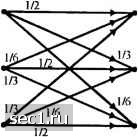Рис. Р.7.3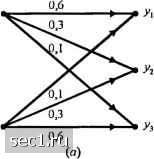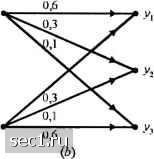

Рис. Р7.4

a) Определите пропускную способность канала в бит/с.

b) Достаточно ли пропускная способность канала для обеспечения передачи речевого сигнала, который стробируется и кодируется посредством логарифмической ИКМ?

c) Обычно канальные искажения, отличные от аддитивного иома, офаничивают скорость передачи по телефонному каналу меньше, чем пропускная способность эквивалентного частотно-офаничснного кшала с АБГШ, рассмотренном в п. (а). Предположим, что на практике достигнута скорость передачи 0,7С 6ci канального кодирования.

Какие из методов кодирования речевого источника, описанные в разделе 3.5, обеспечатцостаточное сжатие, чтобы удовлетворить частотным офаничениям телефонного канала?

7.6. Рассмотрите дискретный канал без памяти (ДКБП) с двоичным входо.м и четверичным выходом, показанный на рис. Р.7.6.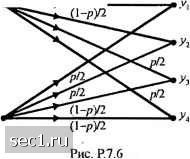

a) определите пропускную способность этого канала;

b) покажите, что этот канал эквивалентен ДСК.

7.7. Определите пропускную способность канала, показанного на рис. 7.7.

Рис. P7.7

7.8. Рассмотрите ДСК с переходной вероятностью ошибки р. Допустим, что 7-это число бит в

кодовых словах, которые представ.ляютсл одним из 2" во-юисных уровней на выходе 1свантоватсля. Определите;

а) вероятность того, »гго кодовое слово, переданное по ДСК, принимается без ошибок; ) вероятность иметь ошибки хотя бы в одном бите (символе?) кодового слова; с) вероятность иметь /; или меньше ошибок в кодовом слове: с1) вычислите вероятность (а), (Ь) и (с) щ\я R = 5, р = 0,01 и п. - 5.

7.!>. Покажите, что дпя ДСК средняя взаилшая информацю! мокду последовательностью Л .\\..„V, канальных входов и соответствмощих канальных вы.ходов удовлетворяют условию

Ф,.а........А,,;К,.Г,.........Y„)f;IfX,;Y,J

с равенством тогда и только тогда, когда символы в последовательности независимы.

7.10. Рис.Р.7.10 иллюстрирует двоичный канал со стиранием с пере.\одны%ш вероятностяли! Р(00) = P(ll) =1- р и Р{ф) = P{el) = р .

Вероятности в.ходных символов равны Р{Х ={)) = а. и 7(.V = l) = l-а.

a) определите среднюю взаимнмо инфор.мацню /(.V,- У) в битах;

b) определите величину а, которая максимизирует I(X;Y), т.е.

обеспечивает пропускную способность канала в бит/символ и постройте С как фуякщпо от р для оптимального значения а;

c) Для вели»шны а, найденной в (Ь), определите взаимщто ин(1юрмацию /(.r;.v)= /(0,0), /(l,l), /(0;е) и /(l.e).

7.11. Рассдютритс канал с двоичным входолг и троичным выходом с переходными вероятностями, показанными на рис. 7.11, где е означают символы стирания.

Для канала с АБГШ величины аир опредсшстгся так: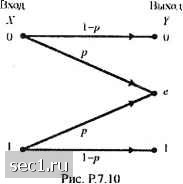

a) определите Rq ддя 0~3 как фун1СЦ1{ю вероятностей аир.

b) параметр скорости Rq зависит от выбора порога в через вероятности аир. Ддя опрсдсленны\ значений i/jVg вели>шну i, которая максимизирует Rg, мо)кно определить методом проб и ошибок. Например, люжно показать, что для SS/Mq нюке О дБ = OfiS-N /2 для 1<£ / <\0, (3 меняется примерно линейно между 0,65-JNq /2 и l.OyJNQ /2 Используя (3 О.бэЛд /2 ддя всей области нарисуйте Rg как ()ун1щшо /Л/,, и сравните этот результат с /?д (• рЦ О = оз)

7.12. Найдите пропускную способность каскадного соединения п двоичных симметричных каналов с одинаковой вероятностью стирания к.