\-p-a

Какова пропускная способность, когда число каналов становится 1 неограниченным?

7.13. Каналы 1, 2 и 3 показаны на рис. Р.7.13.

a) найдите пропускную способность канала I. При каком распределении входа она достигается?

b) найдите пропускную способность канала 2. При каком распределении входа она достигается?

с) Пусть С означает пропускную способность третьего кушала, а С, и I Ст - пропускные способности первого и второго кушала. Какие из следующи.\ соотношений верны и почему?

C<i-(C,+Q) (i)

C = i(C,+C,) (ii)

С>1(С,+С,) (iii)

7.14. Пусть С ознячает пропускную способность дискретного юшала без памяти со входным алфавитом Л - {х, Хт, ...Xf} и вы.чодным алфавитом ~ {У\г Уг Ум} Покажите, что С< min{logM, logvV}.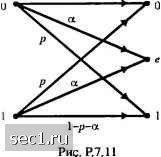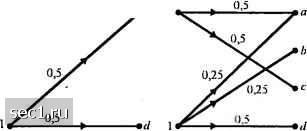

Канал 1

Канал 2 Рис. Р.7.13

Канал 3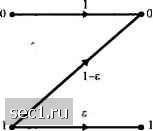

Рис.Р.7.15

7.15. Канал (назовем его Z) показан на рис. Р.7.15.

a) Найдите распределение входов, при котором достигается пропускная способность;

b) Каково распределение входа и пропускная способность кшала для специальных случаев 8 = 0,е = 1ие = 0,5;

c) Покажите, что если л таких каналов соединены каскадно, то результирующий канал эквивалентен каналу Z с 8] =8"

d) Какова пропускная способность эквива.юнтного Z канал;», когд;1

7.16. Найдите пропускную способность канала с АБГШ с полосой частот I МГц, лющностью сигнала К) Вт и спектральной плотностью лющности шума i Ао = 10"т/Гц

7.17. Канал С, - это канал с АБГШ с полосой W, средней мощностью сигнала Р и спектрально!!

плотностью шума Лд. Канал С,- это канал с аддитивным гауссовским шумом с той же полосой и

лющностью сигна-ча, как в канале С,, но со спектральной плотностью лющности шума Ф (/). Далее предположим, что суммарная мощность шума для обоих каналов одинакова, т.е.

W ЦТ

.{f)df-\\N,df = N,W.

-IV -W

Как вы думаете, какой из к<шалов имеет большую пропускную способность? Дайте инт>итивные объяснения.

7.18. Информация от гауссовского источника без памяти с дискретным временем с нулевым средним н

дисперсией a" дол>1<на быть передана по двоичному симметричному каналу с переходной вероятностью ошибки р.

a) Какова минимальная величина достижилюго искажения в месте назначения (иск:1ж-ения измеряются среднеквадратишой ошибкой)?

b) Если канал без памяти с АБГШ, с дискретным временем, с лющностью входа Р и мощностью щмл . каково лшнимально достижилюс исгажение?

c) Теперь предполо)1а1тс, что источник имеет те же базовые свойства, но он с памятью. Уменьшится или увеличится нск11жение при передаче информации по ДСК? Почему?

7.1*). X - это ДВОИЧНЫ!! источник без памяти с Р{Х - О) = 0,3 . Ин()юрмацш! от источника передастся по ДСК с переходной вероятностью р = 0,1.

a) Предположите, что источник непосредственно соединен с каналом, т.е. кодирование не используется. Какова вероятность ош!1бки в месте назначения?

b) Если в !<с1нале произведено кодирование, то какова !Инимaльнo возможная вероятность ошибки npiiHHN!ac\ioro сообщения?

c) При кгпсих значснш!х р возможная надёжная связь (раз) л!еется, с !<одированисА!)?

7.20. Нарисуйте зависимость пропус1а1ой способности от 1/ Л„ для канала с АБГШ, который передаст

двоичные противоположные сигналы и использует на приёме оптимальны!! поэлементный детектор. На тех же осях нарисуйте зависимость пропускной способности того же канала, если передаются двоичные ортогональные сигналы

7.21. В системе связи с кодированием передаются М сообщении 1, 2, ...М = 2* посредством М

вамвых сигналов Jf,(/) , .v,(/) , ... ХдД/) , каждый длительностью пГ. Общая фор.ма дтя сигнала ,Y (/) такова:

-v,(/) = Z/,(/ 7т).

;-г)

где /,Д/) может быть одним из двух сигналов !!ли /,(/), причем f\(J) = f2(J) = при /г[0,/].

Кроме того, предположим, что /, (/) и (/) имеют равную энергию S, а канал идеальный (нет зату.чання) l АБГШ со спектральной плотностью о- значит, ггo пр11Н11маел!ый сигнал г{1) х(/)+ (/). где л{/) - один из сигналов .Y (/) , л (/) - шум.

a) При fi(f) = -foO) покажите, что размерность пространства сигналов .V удовлетворяет )слов1!ю

b) Показ»с1!тс. что в общем N <2п,

c) При М = 2 noKiWcHTC, чго прп общих УД/) н ./,(0

р(ошибкипер. .Y,(/)) < ...j 4p(v\\)p{r\\.jc/v ,

где г. X, и - представления для /"(/), Xj(f) и x{t) в -мерном пространстве, dr - элемент объёма

окажите, что для любого М

/(ошибкн.пер. ,Y„(/))< У J...J 4pir\xjp{r\x„,)Jr .

пространства.

d) Используя результат (с), покажите, что для любого М

1<ш<л/ л"

С) По!сажитс, что

] л/М»1х„,)р(гх„,)/г =ехр

II, следовательно.

/;(ошибкипер. х,„(/)) < ехр

I /и<Л/

БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ

в гл. 7 мы рассмотрели кодирование и декодирование в канале с общей точки зрения и показали, что даже случайно выбранные коды в среднем дают качество, близкое к пропускной способности канала Для случая ортогональных сигналов мы показали, что можно достичь предела пропускной способности канала, если число сигналов не ограничивать.

В этой главе мы опишем специальные коды и рассчитаем их качество для канала с АБГШ. В частности, мы рассмотрим два класса кодов, именно линейные блоковые и свёрточные коды. Качество кода рассчитывается как для декодирования жёстких решений, так и для декодирования мягких решений.

8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ

Блоковый код состоит из набора векторов фиксированной длины, называемых кодовыми словами. Длина кодового слова - это число элементов в векторах, и оно обозначается . Элементы кодового слова выбираются из алфавита с q элементами. Если алфавит содержит два элемента О и 1, код называется двоичным, а элементы любого кодового слова называют битами (двоичными символами). Если элементы кодового слова выбираются из алфавита, имеющего q элементов (q>2), код называют не двоичным. Интересно отметить, что если q является степенью 2, т.е. 7 = 2*, где Л - положительное целое число, каждый q-u элемент имеет эквивалентное двоичное представление, состоящее из h битов и, таким образом, недвоичные коды длины можно отобразить в двоичный код с блоковой длиной п -hN .

В двоичном блоковом коде длиной можно образовать 2" кодовых слов. Из этих 2" кодовых слов мы можем выбрать М = 2*" кодовых слов (< ), чтобы сформировать код. Таким образом, блок из к информационных бит отображается в кодовое слово длины , выбираемое из набора А/ = 2* кодовых слов. Мы обозначим результирующий блоковый код, как код, а отношение Ar/w= определим как скорость кода. В более общем

случае, если код имеет q элементов, можно образовать q" кодовых слов. Подмножество из

Л/ = 2* кодовых слов можно выбрать для передачи к битовых информационных блоков.

Кроме параметра скорости кода R, важным параметром кодового слова является его вес, который равен числу ненулевых элементов, слова. В общем, каждое кодовое слово имеет свой собственный вес. Набор всех весов кода образует распределение весов кода. Когда всеМ кодовых слов имеет одинаковый вес, код называется кодом с фиксированным весом или кодом с постоянным весом. Функции кодирования и декодирования включают арифметические операции суммирования и умножения, выполненные над кодовыми словами. Эти арифметические операции выполняются в соответствии с соотношениями, правилами для алгебраического поля, которое имеет своими элементами символы, содержащиеся в алфавите кода. Для примера, символы в двоичном алфавите равны О и 1, следовательно, поле имеет два элемента. В общем, поле F состоит из набора элементов,