,1-1

g(p)

1 = 1, 2....,k

или, что эквивалентно

P"=Q,(p)g(p) + R,{p), l = \,2,...,k, (8.1.36)

где Qi{p) - частное. Но p"~+R,{p} представляет кодовое слово в циклическом коде, поскольку р" + R{p) = Q,{p)g{p). Следовательно, желательный полином, соответствующий 1-й строке G, равен р" +R,(p).

Пример 8.1.6. Для циклического кода (7,4) с порождающим полиномом Slip) ~ +Р +1 ранее рассмотренного в примере 8.1.5, имеем

р = (р+р+Ыр)+р + 1, р = (р+Ыр)+р"+р+

р =Pg2(p) + P+P P=g2(p)+P + -

Следовательно, порождающая матрица кода в систематической форме

О О

1 о о

и соответствующая проверочная матрица

1 1 1

1 1 1

о 1 1 1

(8.1.37)

1- О

1 О О 1

(8.1.38)

Оставляем в качестве упражнения для читателя показать, что порождающая матрица Gj, даваемая (8.1.35) и матрица G, в систематической форме (8.1.37) генерируют одинаковые наборы кодовых слов (задача 8.2).

Метод конструирования порождающей матрицы G в систематической форме согласно (8.1.36) также подразумевает, что систематический код можно генерировать непосредственно из порождающего полинома g{p). Предположим, что мы умножим полином сообщения х[р) на р"". Тогда получим

p-xip) = х, ,р- +х, ,р"-Ч...+х,р" +х,р"- .

В систематическом коде этот полином представляет первые к бит слова С(р). К этому полиному мы должны прибавить полином степени меньшей, чем п-к, представляющей проверочные символы. Теперь, если р" х(р) разделить на g{p), результат равен

p"-x(p) = 0(p)g(p)+r(p), (8.1.39)

где /"(р) имеет степень меньшую, чем п-к. Ясно, что - это кодовое слово

циклического кода. Следовательно, суммируя (по mod 2) с обеими частями (8.1.39),

мы получаем желаемый систематический код.

Подытоживая, скажем, что систематический код можно генерировать так:

1. Умножаем полином сообщения х{р) на *;

2. Делим р" х{р) на g{p), чтобы получить остаток и

3. Добавляем г(р) к р""х{р).

Ниже мы продемонстрируем, как эти вычисления можно выполнить, используя сдвиговые регистры с обратной связью.

Поскольку р" + \ = g{p)h[p) или, что эквивалентно, g{p)h[p) = О mod(/? +1), мы

видим, что полиномы g[p) и /(/?) ортогональны. Далее, полиномы pg{p) и ph{p)

также ортогональны для всех / и j. Однако, векторы, соответствующие полиномам и

/(/?), ортогональны только, если порядок следования элементов одного из этих векторов реверсировать. То же утверждение применимо к векторам, соответствующим полиномам Ps{p) Р{,р)- Действительно, если проверочный полином h{p) используется как

порождающий для (и, п-к) дуального кода, ансамбль кодовых слов, полученный так,

включают в себя те же кодовые слова, которые генерируются обратным полиномом, за исключением того, что кодовые векторы реверсированы. Это подразумевает, что порождающая матрица для дуального кода, полученная от обратного полинома

может быть также получить непосредственно от hp) Поскольку проверочная матрица И

для циклического кода («, к) является порождающей матрицей для дуального кода,

следует, что Н также можно получить от Следующий пример иллюстрируют это

соотношение.

Пример 8.1.7. Дуальный код для циклического кода (7, 4), порождаемого полиномом g,(p) = +1, - это код (7,3), который порождается обратным полиномом

Р\{р р* + р + Р + \ Однако, мы можем также использовать Л,(р) для получения порождающей матрицы для дуального кода. Матрица, соответствующая полиному рЧ\{р), / = 2, 1,0, равна

1110 10 0 0 1110 10 0 0 1110 1

Порождающая матрица для дуального кода (7, 3), которая является проверочной матрицей для циклического кода (7, 4), состоит из строк G,, взятых в инверсном порядке.

О О 1 О 1 1 Г

Таким образом, Н, = О 1 О 1 1 1 О

10 1110 0

Читатель может убедиться, что G,H=0.

Заметим, что векторы Н, состоит из всех семи двоичных вектор-столбцов длины 3, исключая вектор из одних нулей. Но это как раз описание проверочной матрицы для кода Хемминга (7, 4). Следовательно, циклический код (7, 4) эквивалентен коду Хемминга (7, 4), рассмотренному ранее в примерах 8.1.1 и 8.1.2.

Кодеры для циклических кодов. Операции кодирования при создании циклических кодов можно выполнить при помощи линейных сдвигающих регистров с обратной связью, с использованием порождающего или проверочного полинома. Сначала рассмотрим использование g(p).

Как указано выще, генерирование систематического циклического кода включает три ступени, а именно: умножение полинома сообщения х[р) на р", деление этого произведения на g{p) и в заключение, прибавление остатка г(р) к р"~х(р). Из этих трёх ступеней только деление является нетривиальным.

Деление полинома а{р) = р"х[р) степени и-1 на полином

g{p) = gn-kP"" + gn-k-lP"" +• +>р + go

можно выполнить посредствам (п-к) ячеек регистра сдвига с обратной связью, показанного на рис. 8.1.2.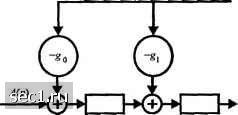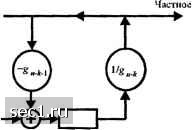

Рис. 8.1.2. Регистр сдвига с обратной связью ддя деления полинома Л(р) на g(p)

Первоначально ячейки сдвига регистра содержит одни нули. Коэффициенты А[р)

поступают и продвигаются по регистру сдвига по одному коэффициенту за такт, начиная с коэффициентов более высокого порядка, т.е. с , затем а„ , и так далее. После

(«-Л:-1)-го сдвига, первый ненулевой выход частного равен Я\ ~ (g„-k) п-: Последующие выходы генерируются так, как показано на рис. 8.1.2. Для образования каждого выходного коэффициента линии мы должны вычесть полином g{p), умноженный

на этот коэффициент, как при обычном «длинном» делении. Это вычитание производится посредством обратной связи. Таким образом, регистр сдвига на рис. 8.1.2 обеспечивает деление двух полиномов.

В нашем случае g„ = go = , и для двоичных кодов арифметические операции выполняются по mod 2. Следовательно, операция вычитания сводится к сложению по mod 2. Далее мы будем только интересоваться генерированием проверочных символов для каждого кодового слова, поскольку код систематический. Как следствие, кодер циклического кода принимает вид, показанный на рис. 8.1.3.