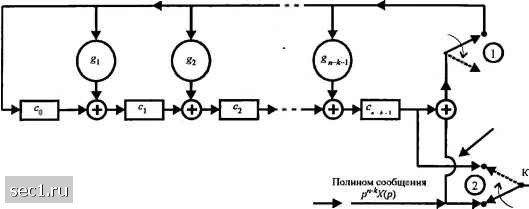Бит проверки на четность

модулятору

Биты сообщения

Рис. 8.1.3. Циклический кодер с использованием порождающего полинома g(p)

Первые к бит на выходе кодера просто равны к информационным битам. Эти к бит одновременно поступают на регистр сдвига, поскольку ключ 1 замкнут. Заметим, что

умножение полиномов р" и х{р) явно не производится. После того как все к

информационных бита попали на вход кодера (и к модулятору), положения двух ключей на рис. 8.1.3 меняются на обратные. Начиная с этого времени, содержимое регистра сдвига просто даёт п-к проверочных символов, которые соответствуют коэффициентам полинома остатка. Эти п-к бита последовательно отправляются на модулятор.

Пример 8.1.8. Регистр сдвига для кодирования циклическим кодом (7,4) с порождающим полиномом р) = +р + 1 показан на рис. 8.1.4.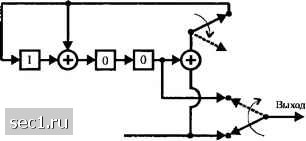

Биты сообщения 0110

Рис. 8.1.4. Циклический кодер (7,4) с использованием порождающего полинома g(p)=p+p+i

Предположим, что сообщением является цепочка ОНО. Содержание сдвигового регистра дано таблицей:

Таким образом, три проверочных символа: 100. Они соответствуют кодовым символам с, =0, Cg = 0 и с, = 1.

Вместо использования порождающего полинома g{p), мы можем выполнить кодер циклического кода, используя проверочный полином

h[p) = p+K +

Соответствующий кодер показан на рис. 8.1.5. Первоначально к информационных символа (бита) передвигаются по регистру сдвига и одновременно поступает на модулятор. После того, как все к информационных символов пройдут по регистру, ключ переводится в положение 2, и сдвиговой регистр работает ещёл-А: такта, генерируя п-к проверочных символов, как показано на рис. 8.1.5.

Биты сообщения

-►•4-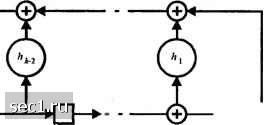

Коаироваииые биты

Рис. 8.1.5. Циклический кодер (nji) с использованием проверочного полинома h(p)

Пример 8.1.9. Проверочный полином для циклического кода (7,4), генерируемый порождающим полиномом = +р + \, равен = р* + р + р + Х. Кодер для этого

кода, основанный на проверочном полиноме, иллюстрируется на рис. 8.1.6. Если на входе кодера действует сообщение ОНО, то проверочными символами являются Cj = 0, =0, - 1, как легко проверить.

Выход

onoooi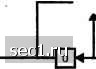

Источник

Рис. 8.1.6. Циклический кодер (7,4) с использованием проверочного полинома h(p)=p*+p+l

Следует заметить, что кодер, базирующийся на порождающем полиноме, проще, когда п-к<к (к>2п), т.е. для больших скоростей кода (i?>i). В то же время кодер, базирующийся на проверочном полиноме, проще, когда к<п-к (A:<tw), что соответствует низкоскоростным кодам {R<\).

Циклические коды Хемминга. Класс циклических кодов включает коды Хемминга, которые имеют длину блока w = 2"-l vl п-к=т проверочных символов, где т - любое положительное целое число. Циклические коды Хемминга эквивалентны кодам Хемминга, описанным в разделе 8.12.

Циклический код Голея (23, 12). Линейный код Голея (23, 12), описанный в разделе (8.1.2), можно генерировать как циклический код посредством порождающего полинома

g{p) = p+p+p+p+p+p + \. . (8.1.40)

Кодовые слова имеют минимальное расстояние d = 7.

Коды сдвигового регистра максимальной длины. Коды сдвигового регистра максимальной длины - это класс циклических кодов

{n,k) = {2"-l,m), (8.1.41)

где т - положительное целое. Кодовые слова обычно генерируются посредством «/-каскадного цифрового регистра сдвига с обратной связью, основанного на проверочном полиноме. Для каждого передаваемого кодового слова т информационных бит вводятся в регистр сдвига, а ключ перемещается с позиции 1 на позицию 2. Содержание регистра сдвигается влево в общей сложности 2" -1 раз. Такая операция генерирует систематический код с требуемой длиной «= 2" 1. Для примера, кодовые слова, генерируемые 3-каскадным регистром сдвига по рис. 8.1.7, сведены в таблицу 8.1.4.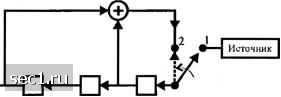

Вы.ход

Рис. 8.1.7. Трёхкаскадный регистр сдвига («=3) с обратной связью

Таблица 8.1.4. Код сдвигового регистра максимальной длины для /о=3

Информационные

биты Кодовые слова

Заметим, что, за исключением кодовых слов из одних нулей, все кодовые слова, генерируемые регистром сдвига, представляют собой циклические сдвиги единственного кодового слова. Это легко увидеть из диаграммы состояний регистра сдвига, которая иллюстрируется на рис. 8.1.8 для т=3. Когда регистр сдвига после первоначального заполнения сдвигается 2™ -1 раз, он проходит через все возможные 2" -1 состояния. Таким образом, регистр сдвига возвращается обратно к начальному состоянию за 2" -1 шагов сдвига.