Этот код имеет минимальное расстояние d =3. Стандартное расположение дано в табл. (8.1.7). Заметим, что в этом коде среди 8 лидеров смежных классов один состоит из одних нулей, пять лидеров имеют вес, равный I и два имеют вес, равный 2. Хотя имеется много больше образцов двойных ошибок, здесь достаточно двух, чтобы заполнить таблицу.

Они были выбраны так, чтобы соответствующие им синдромы отличались от тех, которые соответствуют одиночным ошибкам.

Теперь предположим, что е,. являются лидером смешанного класса, и что было передано кодовое слово С„. Тогда образец ошибки е, приводит к принимаемому кодовому слову

Y = C„+e,.

Синдром равен

S = (c„+e,K=C„ff+е,Н=е.Н\

Ясно, что все принимаемые кодовые слова в тех же смежных классах, образованные из тех же е,, имеют одинаковые синдромы, поскольку последние зависит только от образцов ошибки. Далее, каждый смежный класс, образованный различным е, имеет свой синдром. Установив эти характеристики из стандартного расположения, мы можем просто сконструировать синдромную таблицу декодирования, в которой запишем 2""* синдромов и соответствующие 2""* лидеров смешанных классов, которые представляют образцы ошибок с минимальным весом. Затем, для данного принимаемого кодового вектора Y мы вычисляем синдром

S = YH"

Для вычисленного синдрома S мы находим соответствующий (наиболее правдоподобный) вектор ошибки, скажем ё„. Этот вектор ошибки суммируется с Y. чтобы получить декодированное слово

Пример 8.1.11. Рассмотрим код (5, 2) со стандартным расположением, данным в таблице (8.1.7). Синдромы, соответствующие наиболее правдоподобным образцам ошибок, даны в таблице (8.1.8). Теперь предположим, что действительный вектор ошибок в канале

е=[10 100].

Синдром, вычисленный для этой ошибки, равен S= 001 . Ошибка, определяемая по этому синдрому из таблицы, равна ё= 00001 . Когда ё суммируется с У, результат

11000

10010

приведёт к ошибке декодирования. Другими словами, код (5,2) корректирует все одиночные ошибки и только две двойные ошибки, именно

Табл. 8.1.8. Таблица синдромов для кода (5, 2)

Синдромное декодирование циклических кодов. Как описано выше, декодирование жёстких решений для линейного блокового кода можно выполнить, вычислив сначала синдром S = YH, затем найдя по таблице синдромов наиболее вероятный образец ошибки е, соответствующий вычисленному синдрому S, и, наконец, суммируя образец ошибки е с принятым вектором У, чтобы получить в качестве решения наиболее правдоподобное кодовое слово С. Когда код циклический, вычисление синдрома можно вьтолнить с помощью регистра сдвига, подобного тому, который использовался в кодере.

Для более подробного обсуждения рассмотрим систематический циклический код и

представим принимаемый кодовый вектор У полиномом У{р). В общем Y = С + е, где С-переданное кодовое слово, а е - вектор ошибки. Таким образом, имеем

y{p) = С(р) + е(р) = x(p)g(p) + е(р). (8.1.77)

Теперь разделим y[p) на порождающий полином g{p). Это деление даёт или, что эквивалентно,

Y(p)-Q(p)g{p)+R{p). (8.1.78)

Остаток r{p) - полином степени, меньшей или равной п-к-1. Если объединить (8.1.77) и (8.1.78), получим

е(р) = [Х(р) + Q{p)]g(p) + R{p) . (8.1.79)

Это соотношение показывает, что остаток R{p), полученный отделения У(р) на g{p), зависит только от полинома ошибки е{р) и, следовательно, к{р) - это просто синдром s{p), связанный с образцом ошибки е. Таким образом,

У{р) = Qip)g(p)+S(p), (8.1.80)

где s{p) - полином синдрома степени меньшей или равной п-к-\. Если у(р) делится на gip) точно (без остатка), тогда s{p) = О и принятое слово определяет решение декодера:

Деление на порождающий полином g(p) можно выполнить посредством

регистра сдвига, выполняющего деление, как описано ранее. Сначала принимаемый вектор Y передвигается по (и - А:)-каскадному регистру сдвига, как показано на рис. 8.1.9. Первоначально все ячейки регистра сдвига обнулены, а ключ находится в положении 1. После того как весь принятый «-символьный вектор вошёл в регистр, содержимое и-к ячеек образует синдром в порядке следования символов, указанном на рис. 8.1.9. Эти символы поочерёдно извлекаются из регистра при установке ключа в положение 2. По заданному синдрому от (и - к) -каскадного регистра сдвига и справочной таблице можно идентифицировать наиболее вероятный вектор ошибки.

Пришпый кадовий Bi-KTop

>©-4211-К±)-HZ]-►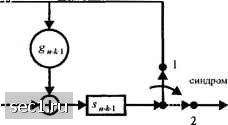

Выходной

Рис. 8.1.9. («-А-)-каскадный регистр сдвига дтя вычисления синдрома

Пример 8.1.12. Рассмотрим вычисление синдрома для циклического кода Хемминга (7,4) с порождающим полиномом g(p) = +Р + 1. Предположим, что принят вектор

Y- 1001101 . Он подаётся на трехкаскадный регистр, показанный на рисунке 8.1.10.

Сдвиг Содержимое регистра

В.чод 1011001

Выходной синдром

ООО 100 010 001 010 101 100 НО

Рис. 8.1.10. Вьргасление синдрома для циклического кода (7,4) с порождающим полиномом g(p)=p3+p+l при принимаемом векторе ¥=[1001101]

После семи сдвигов содержимое регистров сдвига 110, что соответствуют синдрому 011 . Этому синдрому соответствует наиболее правдоподобный вектор ошибки

0001000

1000101

и, следовательно,

С„ =Y + e = Информационные символы 1000.

Метод справочной таблицы, использующей синдром, практически используется тогда, когда п-к мало, например, «-А<10. Этот метод не подходит для многих интересных мощных кодов. Например, если п-к = 20, таблица имеет 2" (примерно 1 миллион) записей. Необходимость хранения большого количества данных и затраты времени, требуемые для обнаружения нужных записей в такой большой таблице, делает метод декодирования со справочной таблицей непрактичным для длинных кодов, имеющих большое число проверочных символов.