кодовых слов, имеющих расстояние / + 1 от переданных кодовых слов. Как следствие, от

(" образцов ошибок с расстоянием / + 1 от каждого кодового слова мы можем

исправить Р,, образцов ошибок. Таким образом, вероятность ошибочного декодирования квазисовершенного кода можно выразить так:

Рм= i:pm+

т=1+2

\.t + V

,-1-1

(8.1.86)

Имеется много известных квазисовершенных кодов, хотя они не существуют для всех наборов пик. Поскольку такие коды оптимальны для двоичного симметричного канала, то любой {п,к) линейный блоковый код должен иметь вероятность ошибки, которая, по крайней мере, принимает значение (8.1.86). Следовательно, (8.1.86) является нижней границей вероятности ошибки декодирования для любого линейного блокового кода (/7,к), где / - наибольшее целое, так чтобы Р,., > О.

Другую пару значений для верхней и нижней границ можно получить, рассматривая два кодовых слова, которые отличаются на минимальное расстояние. Сначала заметим, что Pf не может быть меньше, чем вероятность ошибочного декодирования переданного кодового слова в ближайшее кодовое слово, которое имеет расстояние <i,„ от переданного кодового слова. Т.е.

(8.1.87)

С другой стороны, Рд , не может быть больше, чем умноженная в Ml раз вероятность ошибочного декодирования переданного кодового слова в ближайшее кодовое слово, которое имеет расстояние t/,„ от переданного кодового слова:

. т J

(8.1.88)

"=L..«./2j+l

Когда М велико, нижняя граница (8.1.88) и верхняя граница (8.1.87) весьма далеки одна от другой. Плотную верхнюю границу для можно получить, используя границу Чернова, представленную раньше в разделе 2.1.6. Предположим снова, что передается кодовое слово из одних нулей. При сравнении принимаемого кодового слова с кодовым словом из одних нулей и с кодовым словом веса вероятность ошибки декодирования, полученная из границы Чернова (задача 8.22), ограничена сверху выражением

(8.1.89)

Объединение вероятностей двоичных решений ведет к верхней границе

PmYXA-p)

га=2

(8.1.90) вместо распределения

Более простую версию (8.1.90) можно получить, если взять £/, весов. Т.е.

Р<{М-\\4р{-р\ (8.1.91)

Конечно, (8.1.90) - более плотная граница, чем (8.1.91).

В разделе (8.1.6) мы сравним различные границы, данные выше, для конкретного кода, а именно кода Голея (23, 12).-Дополнительно мы сравним характеристики качества при декодировании жёстких и мягких решений.

8.1.6. Сравнение качества декодированияжёстких и мягких решений

Интересно и поучительно сравнить .границы характеристик качества линейных блоковых кодов в канале с АБГШ при декодировании мягких и жёстких решений.

Для иллюстрации мы используем код Голея (23, 12), который имеет относительно простое распределение весов, данных в таблице 8.1.1. Как было констатировано раньше, этот код имеет минимальное расстояние d = 7. Сначала мы рассчитаем и сравним границы вероятности ошибки при декодировании жёстких решений. Поскольку код Голея (23, 12) является совершенным, точное выражение для вероятности декодирования жёстких решений равно

23 f

23 т

i-p)

23 m

(8.1.92)

где p-вероятность ошибки двоичного элемента в двоичном симметричном канале Предполагается, что для передачи двоичных элементов кодового слова используется двоичная (или четверичная) ФМ и осуществляется когерентная обработка в месте приёма.

При этих условиях соответствующее выражение для р дано в (8.1.13). Дополнительно к точному выражению для вероятности ошибки, даваемое (8.1.92), мы имеем нижнюю границу, даваемую (8.1.81) итри верхние границы, даваемые (8.1.88), (8.1.90) и (8.1.91).

Численные результаты, полученные из этих границ, сравниваются с точным значением вероятности ошибки на рис. 8.1.12.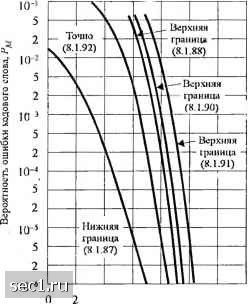

4 6 8 10 12 14 осш на бит, Y4 СдЬ)

Рис. 8.1.12. Сравнение граничны.ч и точных значений вероятности ошибки для декодирования жёстких решений для кода Голея (23,12)

Видим, что нижняя граница очень свободная. При = lu нижняя граница отличается примерно на 2 дБ по сравнению с точным значением вероятности ошибки. При

= 10 разница увеличивается примерно до 4 дБ. Из трёх верхних границ наиболее плотная та, которая определяется (8.1.88); она отличается меньше, чем на 1 дБ по сравнению с точным значением вероятности ошибки при /, = 10". Граница Чернова (8.1.90), которая использует распределения весов, также относительно плотная. Наконец,

граница Чернова, которая использует только минимальное кодовое расстояние, наихудшая из трёх. При Рд, = 10 она отличается от точного значения вероятности ошибки примерно на 2 дБ. Все три верхние границы очень неточные для значений вероятности ошибки выше

Интересно также сравнить характеристики качества при декодировании мягких и жёстких решений. Для этого сравнения мы используем верхние границы для вероятности ошибки при декодировании мягких решений, даваемые (8.1.52), и точное выражение для вероятности ошибки для декодирования жёстких решений, определяемое (8.1.92). Рис. 8.1.13 иллюстрирует эти характеристики качества.

Мы видим, что две границы для декодирования мягких решений отличаются примерно на 0,5 дБ при = 10 и примерно на

10-2 5 2

10- 5

10-" р

i 5

I 2

М ,0 5

0 2 4 6 8 О 2 14 ОСШ ш бит, Y4 (дБ)

Рис. 8.1.13. Сравнение декодирокшия мягких и жёстких решений для кода Голея (23,12)

1 дБ при Рд, = 10. Мы также видим, разница в качестве декодирования жёстких и мягких решений примерно равна 2 дБ в области 10 <Рд/<10-. В области Рд, >10" кривая вероятности ошибки при декодировании с жестким решением пересекает кривые для границ вероятности ошибки при декодировании мягких решений. Такое поведение указывает на то, что границы для декодирования мягких решений неточные, когда Pд > 10 ".

Разница в 2 дБ (по ОСШ на бит) между декодированием жёстких и мягких решений применима не только для кода Голея, но является фундаментальным результатом, который применим в общем к кодированию в системах цифровой связи в каналах с АБГШ. Этот результат получен ниже при расчёте пропускной способности канала с АБГШ при декодировании жёстких и мягких решений.

Пропускная способность ДСК в битах/символ, полученная в разделе 7.1.2, равна

C-l + ;;log,;; + (l-p)log3(l-;;), (8.1.93)

где вероятность ошибочного приёма двоичного элемента р при использовании когерентной ФМ в канале с АБГШ определяется (8.1.13). Предположим, что мы используем (8.1.13) для р, и пусть С= R. в (8.1.93), и тогда определим у,, которое удовлетворяет уравнению. Результат показан на рис. 8.1.14 в форме кривой зависимости R от у. Например, предположим, что мы хотим использовать код со скоростью R = 2 Для этой скорости кода видим, что минимальное значение ОСШ на бит, требуемое для достижения пропускной способности канала при декодировании жёстких решений, равно примерно 1,6 дБ

Каков предел ОСШ на бит, когда скорость кода стремится к нулю? Для многих значений R вероятность р можно аппроксимировать так:

Р«1-л/уЛ/ (81-94)

Если выражение для р подставить в (8.1.93), а логарифм в (8.1.93) аппроксимировать