log,.(l + x)(x-b)/ln2.

формула для пропускной способности канала сводится к

Теперь положим С . Тогда, в пределе, когда R ->0, получаем результат

y,=i7iln2 (0,37 дБ). (8.1.96)

Пропускную способность канала с АБГШ с двоичным входом при декодировании мягких решений можно вычислить аналогичным образом. В разделе 7.1.2 мы привели выражение для пропускной способности (в битах на кодовый символ) для этого случая

(8.1.97)

где p{y{f(), к -Q,\, означает ФПВ для выхода демодулятора при условии, что передан, соответственно, символ О или 1. Для канала с АБГШ имеем

1 {у....?/2а

р(ук) =

к 0,1,

(8.1.98)

где /н„ = -д/, W - , а = \Nq и \ = РЦ,. Безусловная плотность вероятности р{у) определяется половиной суммы (yll) и р(>о). Поскольку 7? стремится к нулю, выражение (8.1.97) для пропускной способности канала можно аппроксимировать формулой

C~yRj\n2. (8.1.99)

Опять предположим C = R. Таким образом, когда Л->0, минимальное значение ОСШ на бит, требуемое для достижения пропускной способности, равно

-1п2 ( 1,6 дБ). (8.1.100)

Используя (8.1.98) в (8.1.97) и положив С - R можно получить численное решение для скорости кода в области 0< R<\. Результат этих расчётов также показан на рис. 8.1.14.

Из вышеизложенного следует, что в пределе, когда 7?. стремится к нулю, разница в ОСШ Уь между

декодированием жёстких и мягких решений равна \т1, что приближённо равно 2 дБ. С другой стороны, по мере увеличения Л до единицы, разница в Уь для двух разновидностей декодирования уменьшается.

. 1 о

\ 0,6 о.4 о 0,2 О

Д: ксдпрокание мягюк решении

Декодирование жестких решений

I I I I

2 -1 01 23456 Минимальное ОСШ на бит, у, (дБ)

Рис. 8.1.14. Скорость кода как функция минимального ОСШ на бит при декодировании мягких и жёстких решений

Например, при R - 0,8 разница примерно равна 1,5 дБ. Кривые на рис. 8.1.14 дают больше информации, чем только разницу в качестве между декодированием мягких и жёстких решений. Эти кривые подробно определяют требуемые значения минимума ОСШ для данной скорости кода. Например, скорость кода R = 0,8 может обеспечить сколь угодно малую вероятность ошибки при ОСШ на бит 2 дБ, если используется декодирование мягких решений.

Для сравнения заметим, что двоичная ФМ при отсутствии кодирования требует 9,6 дБ для достижения вероятности ошибки 10. Следовательно, возможен выигрыш в 7,6 дБ при использовании скорости кода Re = i. К сожалению, для достижения такого большого вьи1грыша за счёт кодирования обычно требуется применение очень длинных кодовых блоков, которые ведут к очень сложному приёмнику. Тем не менее, кривые рис. 8.1.14 дают оценку для сравнения выигрыша кодирования, достигаемого практически реализуемыми кодами с основными ограничениями при декодировании мягких или жёстких решений.

Вместо сравнения различия между декодированием жёстких и мягких решений, основанного на соотношениях пропускной способности канала, мы можем делать такие же простые сравнения, основанные на параметрах скорости при случайном кодировании. В главе 7 мы показали, что средняя вероятность ошибки по ансамблю случайно выбранных двоичных кодовых слов имеет верхнюю границу

Р<2

(8.1.101)

где = к/п - скорость кода, а предельная скорость R связывает верхнюю границу с R так. что при -> 00. Для неквантованного декодирования (мягких решений) R

определяется так

(8.1.102)

1 + е /No

где 6/Nq = Rj/ - ОСШ на измерение. Этот результат бьш ползчен в разделе 7.2.

С другой стороны, если выход демодулятора квантуется на О уровней до декодирования, то границу Чернова можно использовать в качестве верхней границы для усреднённой по ансамблю вероятностей двоичной ошибки i(s„s„,), данной в разделе 7.2 Результат такого расчёта - та же верхняя граница для Р, определённая по (8.1.101), но с , заменой R т Rg, где

Rp = max-jj

-log.Z

(8.1.103)

В (8.1.103) {Pj}- априорные вероятности-двух сигналов на входе канала и {P(j\j)} означают переходные вероятности канала. Например, для слзая ДСК и Рх= Pq=\, p(oo)-/(ll)=l-/; и р[о\\)=р{\\о) = р следует

RQ=\og,--Т==, 0 = 2, (8.1.104)

P-Q{4nK)- (8.1.105)

Кривые Rq в зависимости от 101g(g/iVg) иллюстрируется на рис. 8.1.15 для = 2 и Q=qo (декодирование мягких решений).

Заметим, что разница в качестве декодирования между неквантованным декодированием мягких решений и декодированием жёстких решений приблизительно равно 2дБ. Фактически, снова можно легко показать, что при S/Nq->0 потеря в

качесгве, обусловленная декодированием жёстких решений, равна 101g(я/2)«2дБ, что являегся той же разницей в децибелах, которая была получена в нашем сравнении при

использовании соотношений для пропускной способности канала. Напомним, что около 1 дБ этих потерь можно восполнить квантованием выхода демодулятора на трёх уровнях вместо двух (см. задачу 7.11). Дополнительное улучшение возможно путём квантования выхода демодулятора на число уровней, большее трёх, как показано в разделе 7.3.

?Г 0,9 I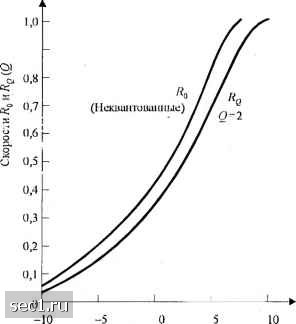

-5 О

Рис. 8.1.15. Сравнение Сдекодпрование мяпси.х решений) с Rg (декодирование жёстких решений) в функции от ОСШ на измерение

8.1.7. Границы для минимальных расстояний линейных блоковых кодов

Выражения для вероятности ошибки, полученные в этой главе для декодирования мягких и жёстких решений линейных двоичных блоковых кодов, ясно указывает на важное значение параметра минимальное кодовое расстояние для качества кода. Если мы, например, рассмотрим декодирование мягких решений, верхняя граница вероятности ошибки, представленная в (8.1.52), указывает на то, что для заданной скорости кода R-klii вероятность ошибки в канале с АБГШ уменьшается экспоненциально с Если эту границу использовать в соединении с нижней границей для d, данной ниже, мы получаем верхнюю границу для Рд, которую можно достичь многими известными кодами. Аналогично, мы можем использовать верхнюю границу данную в (8.1.82) для вероятности ошибки при декодировании жёстких решений в соединении с нимсней границей для для получения верхней границы для вероятности ошибочного

декодирования линейных двоичных блоковых кодов в ДСК.

С другой стороны, верхнюю граница для d можно использовать для определения нижней границы вероятности ошибки, достигаемой наилучшими кодами. Для примера, предположим, что используется декодирование жёстких решений. В этом случае мы имеем две нижние границы для Р,,, даваемые (8.1.86) и (8.1.87), причём первая более плотная. Если хотя бы одна из этих границ использовалась совместно с верхней границей для то результатом будет нижняя граница для Р,, для наилучшего {ri,k) кода. Таким образом, верхние и нижние границы с б/, очень важны для оценки эффективности кодов.