Простая верхняя граница для минимального расстояния двоичного или недвоичного линейного блокового кода {п,к) была дана в (8.1.14) как d<n~k + l. Удобно нормировать это выражение через длину блока л/. Это даёт

<(l-PJ + , • (8.1.106)

где - скорость кода. Для больших слагаемым 1 / п можно пренебречь. Если код имеет наибольшее возможное расстояние, т.е. t/„ =п- к + 1, его назьшают разделимым кодом с .макашальиым расстоянием. Исключая случаи тривиального кода (и, 1) для передачи двоичных сообщений с повторением, не существует двоичных разделимых кодов с максимальным расстоянием. Фактически верхняя граница в (8.1.106) для двоичных кодов весьма неточная. С другой стороны, существуют недвоичные коды с d=n-к + 1. Например, коды Рида-Соломона, которые представляют подкласс БЧХ кодов, являются разделимыми кодами с максимальным расстоянием. В дополнение к верхней границе, данной выше, имеется несколько плотных границ для минимального расстояния линейных блоковых кодов. Мы вкратце опишем четыре важные границы, три из них верхние границы, а четвертая нижняя. Доказательство этих границ сложное и не представляет особого интереса в нашем последующем обсуждении. Интересующемуся читателю можно порекомендовать главу 4 книги Питерсона и Уэлдона (1972) с этими доказательствами.

Одна верхняя граница для минимальных расстояний может получиться из неравенства (8.1.83). Взяв логарифм от обеих частей (8.1.83) и разделив на п, мы получим

1-я -logoЕ . (8.1.107)

Поскольку эффективность кода, измеряемая параметром /, связана с минимальным расстоянием, (8.1.107) является верхней границей для минимального расстояния. Ее называют верхней грашщей Хем.минга.

Получена асимптотическая форма (8.1.107) при и-> оо. Теперь для любого п пусть является наибольшим целым /, при котором выполняется (8.1.107). Тогда можно показать (Питерсон и Уэлдон, 1972) что при оо отношение « для каждого {пЛ) блокового кода не может превысить /ц /, где tln удовлетворяет условию

\-R = H{tJfi), (8.1.108)

а Я(-) - двоичная энтропийная функция, определяемая (3.2.10).

Обобщение границы Хемминга на недвоичные коды с основанием q простое:

l-,>-log,

,=0 Vy

(8.1.109)

Другую верхнюю границу, открытую Плоткиным (I960), можно определить так. Число проверочных символов, требуемое для достижения минимального расстояния d в линейном блоковом коде iti,k), удовлетворяет неравенству

Для двоичного кода (8.1.110) можно выразить так

п-к>

"-l-log,„,„

(8.1.110)

2с/„

l0g2m,r.

в пределе, когда н->оо,при dln<\ (8.1.110) приводит к

(8.1.111)

Наконец, имеется другая плотная верхняя граница для минимального расстояния, полученная Элиасом (Берлекэмп, 1968). Её можно выразить в асимптотической форме:

dJ,i<2A{\-A), (8.1.112)

где параметр А связан со скоростью кода уравнением

R = \ + A\og2A+{\-A)\Q§J\-A\ 0<А<\. (8.1.113) Существуют также нижние границы для минимального расстояния линейного блокового кода {п,к). В частности, существует двоичный блоковый код, имеющий

нормированное минимальное расстояние, которое асимптотически удовлетворяет неравенству

™пАа, (8.1.114)

где а связано со скоростью кода уравнением

7? = l-(a) = l + alog2a + (l-a)log2(l-a), 0<а<. (8.1.115)

Эта нижняя граница - частный случай нижней границы, открытой Гильбертом (1952) и Варшамовым (1957), которая применима для недвоичных и двоичных блоковых кодов.

Асимптотические границы, данные выше, приведены на рис. 8.1.16 для двоичных кодов. С целью сравнения на рисунке даны также кривые минимального расстояния, как функции скорости кода для БЧХ кодов с длиной блоков и = 31 и 63.

Видно, что для « = 31 и 63 нормированное минимальное расстояние хорошо ложится над нижней границей Варшамова-Гильберта. Но мере увеличения длины блока , эффективность БЧХ кодов ослабевает. Например, когда = 1023 , кривая нормированного минимального расстояния ложится близко к границе Варшамова-Гильберта. Если п возрастает выше « = 1023 , нормированное минимальное расстояние БЧХ кода продолжает уменьшается и падает ниже границы Варшамова-Гильберта. Это значит, что („„„Д/ приближается к нулю по мере того как п стремится к бесконечности. Следовательно, БЧХ коды, которые являются наиболее важным классом циклических кодов, не очень эффективны при больших длинах блоков.

Ч \ Коды БЧХ. й-бЗ

.\11яя граница Плоткипа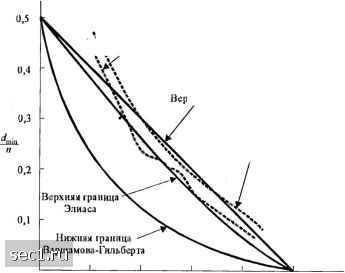

Коды БЧХ, п=31

Рис. 8 1

1,11

0,2 (1,4 0,6

Скорость кода

16. Верхняя и нижняя границы иоркшровшиюго инимaлLHOгo расстояния в фующии от скорости кода

8.1.8. Недвоичные блоковые коды и каскадные блоковые коды

Недвоичные блоковые коды состоят из набора кодовых слов фиксированной длины, в которых каждый элемент кодового слова выбирается из алфавита, содержащего q

символов, обозначаемых {О, 1, 2,...,</-!}. Обычно / = 2*, так что к информационных бит отображается одним из q символов. Длина недвоичного кодового слова обозначается через Л, а число информационных символов, закодированных блоком из N символов, обозначается К. Минимальное расстояние недвоичного кода обозначается .

Систематический блоковый код (Л/, АГ) содержит информационных символов и N К проверочных символов.

Среди различных типов недвоичных линейных блоковых кодов коды Рида-Соломона являются одними из самых важных для практических приложений. Как было указано раньше, они составляют подкласс БЧХ кодов, которые, в свою очередь, являются классом циклических кодов. Эти коды описываются параметрами

N = q-\ = 2 \

к = \, 2, 3,...Л-1 R, = K/N

Такой код гарантированно исправляет до

ошибок символов. Конечно, эти коды могут быть расширены и укорочены так, как было описано ранее для двоичных блоковых кодов.

Распределение весов {А} класса кодов Рида-Соломона известно. Коэффициенты во взвешивающем полиноме определяются так:

; )™„, (8.1.118)

\ J У

где = и 7 = 2*.

Одно объяснение важности кодов Рида-Соломона - их хорошие дистанционные свойства. Второе объяснение их важности - существование эффективных алгоритмов декодирования жёстких решений, которые делают возможным реализовать относительно длинные коды во многих практических приложениях, где требуется кодирование.

Недвоичный код хорошо согласован с техникой М-ичной модуляции для передачи 2 возможных символов. В частности, часто используется М-ичная ортогональная система сигналов, например, М-ичная ЧМ. Каждый из 2* символов в /-ичном алфавите отобрах<ается в один из М = 2* ортогональных сигналов. Таким образом, передача кодового слова связана с передачей N ортогональных сигналов, где кахедый сигнал выбирается из набора М - 2* возможных сигналов.

Оптимальный демодулятор для такого сигнала, искажённого в канале с АБГШ, состоит из М согласованных фильтров (или взаимных корреляторов) чьи выходы подаются к декодеру в форме мягких или жёстких решений. Если демодулятор вынес жёсткие решения, то вероятность ошибки символа Р и параметры кода достаточны для характеристики качества декодера. Действительно, модулятор, канал с АБГШ и демодулятор формируют эквивалентный симметричный канал без памяти с дискретным (М-ичным) входом и дискретным (М-ичным выходом, характеризуемый переходными